Questions: Solve for P. Express your answer in simplest and exact form. s = c P^2 m^2 t for P > 0 P =

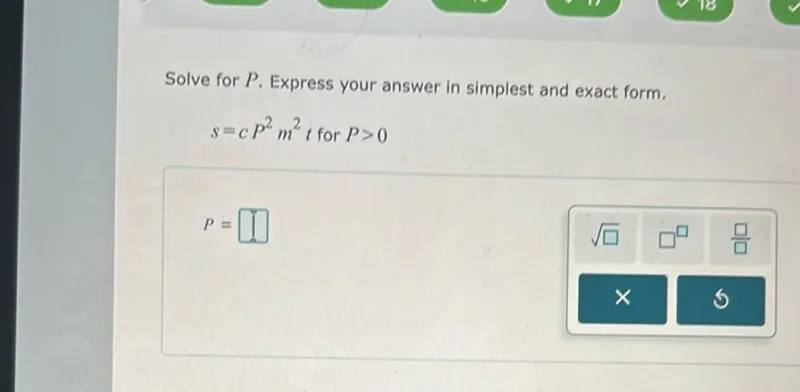
Solve for \( P \) in the equation \( s = c P^{2} m^{2} t \).

Rearranging the equation.

To isolate \( P \), we can rearrange the equation as follows: \[ P^{2} = \frac{s}{c m^{2} t} \]

Taking the square root of both sides.

Since \( P > 0 \), we take the positive square root: \[ P = \sqrt{\frac{s}{c m^{2} t}} \]

\(\boxed{P = \sqrt{\frac{s}{c m^{2} t}}}\)

Express \( P \) in terms of \( m \) using the inverse function.

Identifying the inverse function.

The inverse function derived from the equation is: \[ s^{-1}(m) = \pm \frac{\sqrt{\frac{m}{c t}}}{P} \]

Expressing \( P \) in terms of \( m \).

From the inverse function, we can express \( P \) as: \[ P = \frac{\sqrt{\frac{m}{c t}}}{s^{-1}(m)} \]

\(\boxed{P = \frac{\sqrt{\frac{m}{c t}}}{s^{-1}(m)}}\)

\(\boxed{P = \sqrt{\frac{s}{c m^{2} t}}}\)

\(\boxed{P = \frac{\sqrt{\frac{m}{c t}}}{s^{-1}(m)}}\)