Questions: A cell phone manufacturer tests the battery lifetimes of its cell phones by recording the time it takes for the battery charges to run out while testers are streaming videos on the phones continuously. The manufacturer claims that the population mean of the battery lifetimes of all phones of their latest model is 5.74 hours. As a researcher for a consumer information service, you want to test that claim. To do so, you select a random sample of 45 cell phones of the manufacturer's latest model and record their battery lifetimes. Assume it is known that the population standard deviation of the battery lifetimes for that cell phone model is 2.42 hours. Based on your sample, follow the steps below to construct a 90% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. Then state whether the confidence interval you construct contradicts the manufacturer's claim. (a) Click on "Take Sample" to see the results from your random sample of 45 phones of the manufacturer's latest model. Number of phones Sample mean Sample standard deviation ------------ ------------- ------------- 45 5.47 2.13 Population standard deviation ------------ 2.42 Enter the values of the sample size, the point estimate for the population mean; the population standard deviation, and the critical value you need for your 90% confidence interval. (Choose the correct critical value from the table of critical values provided.) When you are done, select "Compute". Sample size: Point estimate: Standard error: Population standard deviation: Critical value: Compute (b) Based on your sample, graph the 90% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. - Enter the lower and upper limits on the graph to show your confidence interval. - For the point (4), enter the manufacturer's claim of 5.74 hours.

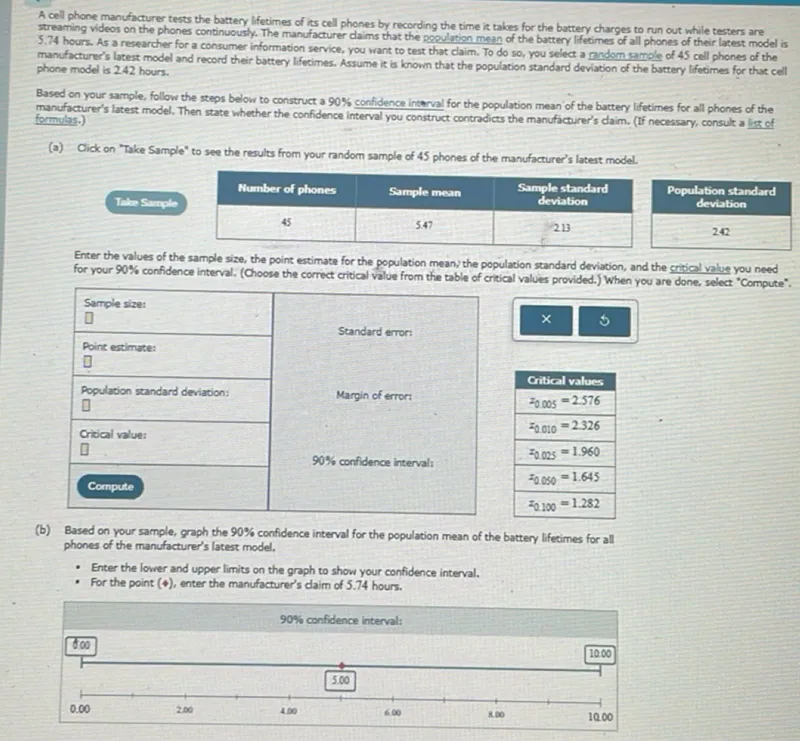
A cell phone manufacturer tests the battery lifetimes of its cell phones by recording the time it takes for the battery charges to run out while testers are streaming videos on the phones continuously. The manufacturer claims that the population mean of the battery lifetimes of all phones of their latest model is 5.74 hours. As a researcher for a consumer information service, you want to test that claim. To do so, you select a random sample of 45 cell phones of the manufacturer's latest model and record their battery lifetimes. Assume it is known that the population standard deviation of the battery lifetimes for that cell phone model is 2.42 hours. Based on your sample, follow the steps below to construct a 90% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. Then state whether the confidence interval you construct contradicts the manufacturer's claim. (a) Click on "Take Sample" to see the results from your random sample of 45 phones of the manufacturer's latest model. Number of phones Sample mean Sample standard deviation ------------ ------------- ------------- 45 5.47 2.13 Population standard deviation ------------ 2.42 Enter the values of the sample size, the point estimate for the population mean; the population standard deviation, and the critical value you need for your 90% confidence interval. (Choose the correct critical value from the table of critical values provided.) When you are done, select "Compute". Sample size: Point estimate: Standard error: Population standard deviation: Critical value: Compute (b) Based on your sample, graph the 90% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. - Enter the lower and upper limits on the graph to show your confidence interval. - For the point (4), enter the manufacturer's claim of 5.74 hours.
Transcript text: A cell phone manufacturer tests the battery lifetimes of its cell phones by recording the time it takes for the battery charges to run out while testers are streaming videos on the phones continuously. The manufacturer claims that the population mean of the battery lifetimes of all phones of their latest model is 5.74 hours. As a researcher for a consumer information service, you want to test that claim. To do so, you select a random sample of 45 cell phones of the manufacturer's latest model and record their battery lifetimes. Assume it is known that the population standard deviation of the battery lifetimes for that cell phone model is 2.42 hours. Based on your sample, follow the steps below to construct a $90 \%$ confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. Then state whether the confidence interval you construct contradicts the manufacturer's claim. (a) Click on "Take Sample" to see the results from your random sample of 45 phones of the manufacturer's latest model. \begin{tabular}{|c|c|c|} \hline Number of phones & Sample mean & \begin{tabular}{c} Sample standard \\ deviation \end{tabular} \\ \hline 45 & 5.47 & 2.13 \\ \hline \end{tabular} \begin{tabular}{|c|} \hline \begin{tabular}{c} Population standard \\ deviation \end{tabular} \\ \hline 2.42 \\ \hline \end{tabular} Enter the values of the sample size, the point estimate for the population mean; the population standard deviation, and the critical value you need for your $90 \%$ confidence interval. (Choose the correct critical value from the table of critical values provided.) When you are done, select "Compute". \begin{tabular}{|l|l|} \hline Sample size: & \\ \hline$\square$ & \\ \hline Point estimate: & \\ \hline$\square$ & Standard error: \\ \hline Population standard deviation: & \\ \hline$\square$ & \\ \hline Critical value: & \\ \hline$\square$ & \\ \hline Compute & \\ \hline \end{tabular} (b) Based on your sample, graph the $90 \%$ confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. - Enter the lower and upper limits on the graph to show your confidence interval. - For the point ( 4 ), enter the manufacturer's claim of 5.74 hours.
failed

Solution

failed
failed

Solution Steps

Step 1: Identify the given information

Sample size (n) = 45 Sample mean (x̄) = 5.47 Population standard deviation (σ) = 2.42 Confidence level = 90% Manufacturer's claim (µ) = 5.74 hours

Step 2: Calculate the critical value

For a 90% confidence interval, the alpha level (α) is 1 - 0.90 = 0.10. Since we are constructing a two-tailed confidence interval, we divide alpha by 2: α/2 = 0.10 / 2 = 0.05. We look up the z-score corresponding to 0.05 in a standard normal distribution table or use a calculator. The critical value is approximately 1.645.

Step 3: Calculate the margin of error

Margin of Error = Critical value * (Population standard deviation / sqrt(Sample size)) Margin of Error = 1.645 * (2.42 / sqrt(45)) Margin of Error ≈ 1.645 * (2.42 / 6.708) Margin of Error ≈ 1.645 * 0.361 Margin of Error ≈ 0.594

Step 4: Calculate the confidence interval

Lower Limit = Sample mean - Margin of Error Lower Limit = 5.47 - 0.594 Lower Limit ≈ 4.88

Upper Limit = Sample mean + Margin of Error Upper Limit = 5.47 + 0.594 Upper Limit ≈ 6.06

Step 5: Graph the confidence interval and the manufacturer's claim

The 90% confidence interval is approximately (4.88, 6.06). The manufacturer's claim of 5.74 hours falls within this interval.

Step 6: Determine if the confidence interval contradicts the claim

Since the manufacturer's claim of 5.74 hours falls within the calculated 90% confidence interval (4.88, 6.06), the confidence interval does not contradict the manufacturer's claim.

Final Answer

Sample size: 45 Point estimate: 5.47 Population standard deviation: 2.42 Critical value: 1.645 Confidence Interval: (4.88, 6.06) The confidence interval does not contradict the manufacturer's claim. \\(\boxed{(4.88, 6.06)}\\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Which kind of animal does the author NOT see on the trip to Antarctica? Select one answer. A penguin B huge white bird c elephant seal D great white shark
failedAnswered
HCl + CaCO3 → CaCl2 + H2O + CO2
failedAnswered
9) From Lesson 7, Q1: While great for the economic health of the continent, the expansion of trade was one of the best and worst things that happened to Europe in the Middle Ages because of: a) People didn't have enough money b) Not enough ways to travel c) Peoples' voyages brought sickness and global epidemics d) More issues than can be counted
failedAnswered
1a. On what open intervals is f(x) increasing? -3<x<3 1b. On what open intervals is f(x) concave down? 0<x<0.5 1c. On what interval is the rate of change of f(x) negative and decreasing? -6<x<-3
failedAnswered
A figura a seguir representa a interação entre uma espécie de fungo filamentoso e as raízes de uma gramínea. Essa associação é chamada de micorriza, na qual as hifas dos fungos conectam-se às ramificações das raízes e otimizam a capacidade de absorção de água e de nutrientes que essas estruturas têm. Um exemplo de nutriente que tem sua absorção otimizada por meio dessa associação é o fósforo. Disponível em: https://www.cropscience.bayer.us. Acesso em: 7 maio. 2024. (adaptado) Na planta, o nutriente citado participa da constituição dos(as) A. bases nitrogenadas, que estão presentes nas moléculas de DNA. B. moléculas de ATP, que fornecem energia para as células. C. aminoácidos, que são as unidades básicas das proteínas. D. polímeros de celulose, que compõem a parede das células. E. monômeros do amido, que formam a reserva energética das plantas.