Questions: Follow the directions to solve the system of equations by elimination. 8x + 7y = 39 4x - 14y = -68 1. Multiply the first equation to enable the elimination of the y-term. 2. Add the equations to eliminate the y-terms. 3. Solve the new equation for the x-value. 4. Substitute the x-value back into either original equation to find the y-value. 5. Check the solution. The solution to the system of equations is ( . ).
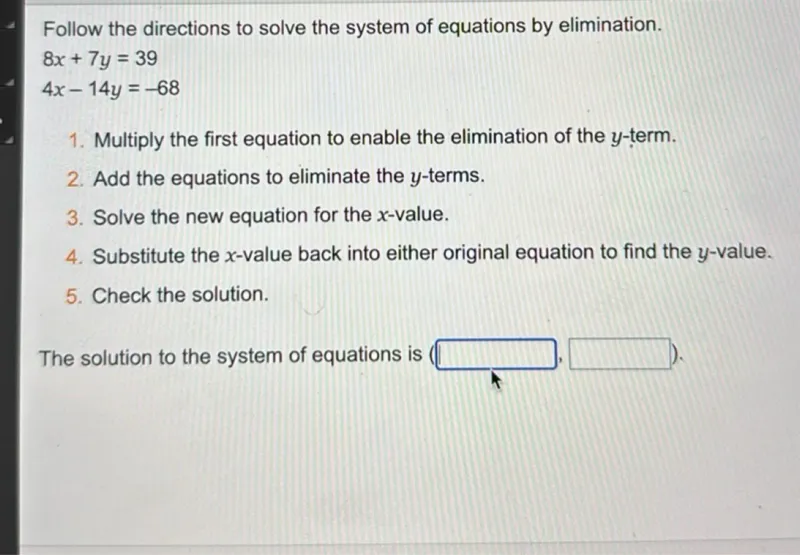
Transcript text: Follow the directions to solve the system of equations by elimination.
\[
\begin{array}{l}
8 x+7 y=39 \\
4 x-14 y=-68
\end{array}
\]
1. Multiply the first equation to enable the elimination of the $y$-term.
2. Add the equations to eliminate the $y$-terms.
3. Solve the new equation for the $x$-value.
4. Substitute the $x$-value back into either original equation to find the $y$-value.
5. Check the solution.
The solution to the system of equations is ( $\square$ . $\square$ ).





