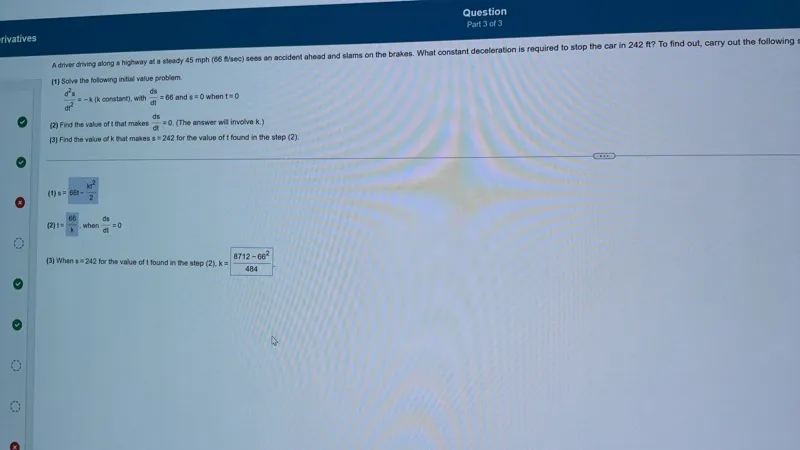
Questions: Question Part 3 of 3 Derivatives (1) Solve the following initial value problem. The second derivative of s with respect to t is equal to -k (k constant), with the first derivative of s with respect to t equal to 66 and s equals 0 when t equals 0. (2) Find the value of t that makes the first derivative of s with respect to t equal to 0. (The answer will involve k.) (3) Find the value of k that makes s equal to 242 for the value of t found in step (2). (1) s equals 66t minus k times t squared over 2 (2) t equals 66 over k, when the first derivative of s with respect to t equals 0 (3) When s equals 242 for the value of t found in step (2), k equals (8712 minus 66 squared) over 484.

Solution Steps

We start with the second-order differential equation given by \[ \frac{d^{2}s}{dt^{2}} = -k. \] Integrating this equation once, we obtain \[ \frac{ds}{dt} = -kt + C_2, \] where \( C_2 \) is a constant of integration. Applying the initial condition \( \frac{ds}{dt} = 66 \) when \( t = 0 \), we find \( C_2 = 66 \). Thus, we have \[ \frac{ds}{dt} = -kt + 66. \]

Integrating again, we get \[ s = -\frac{kt^2}{2} + 66t + C_1. \] Using the initial condition \( s = 0 \) when \( t = 0 \), we find \( C_1 = 0 \). Therefore, the solution for \( s(t) \) is \[ s(t) = -\frac{kt^2}{2} + 66t. \]

To find the value of \( t \) that makes \( \frac{ds}{dt} = 0 \), we set the first derivative equal to zero: \[ -k t + 66 = 0. \] Solving for \( t \), we find \[ t = \frac{66}{k}. \]

Next, we substitute \( t = \frac{66}{k} \) into the expression for \( s(t) \) and set it equal to 242: \[ s\left(\frac{66}{k}\right) = -\frac{k}{2}\left(\frac{66}{k}\right)^2 + 66\left(\frac{66}{k}\right) = 242. \] Simplifying this equation, we have \[ -\frac{66^2}{2k} + \frac{66^2}{k} = 242. \] This simplifies to \[ \frac{66^2}{2k} = 242. \] Solving for \( k \), we find \[ k = \frac{66^2}{484} = 9. \]

Final Answer