Questions: Convert to an exponential equation. z = logm R^3 The equivalent equation is □ (Type in exponential form.)
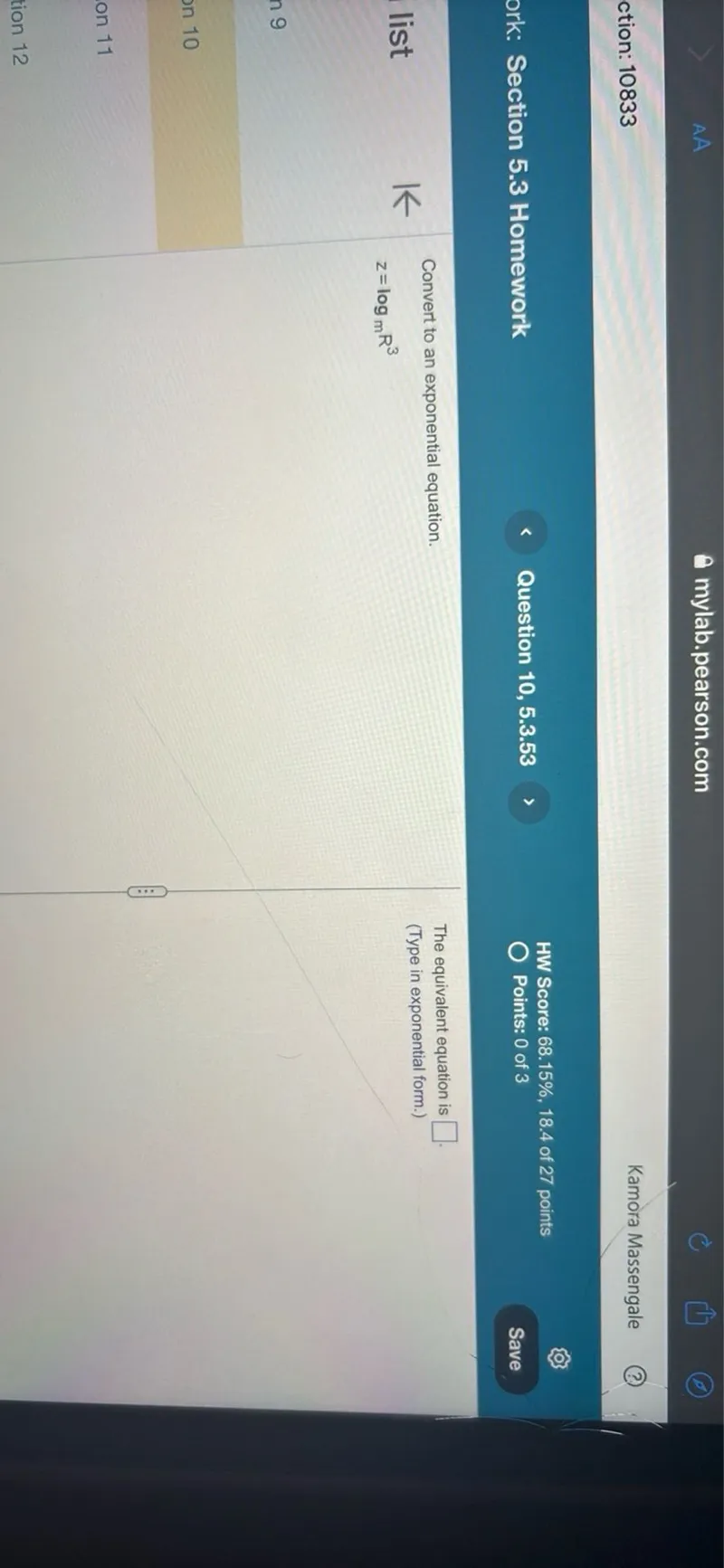
Transcript text: Convert to an exponential equation.
\[
z=\log _{m} R^{3}
\]
The equivalent equation is $\square$
(Type in exponential form.)





