Questions: Hawa is flying a kite, holding her hands a distance of 3.75 feet above the ground and letting all the kite's string out. She measures the angle of elevation from her hand to the kite to be 26 degrees. If the string from the kite to her hand is 135 feet long, how many feet is the kite above the ground? Round your answer to the nearest tenth of a foot if necessary.
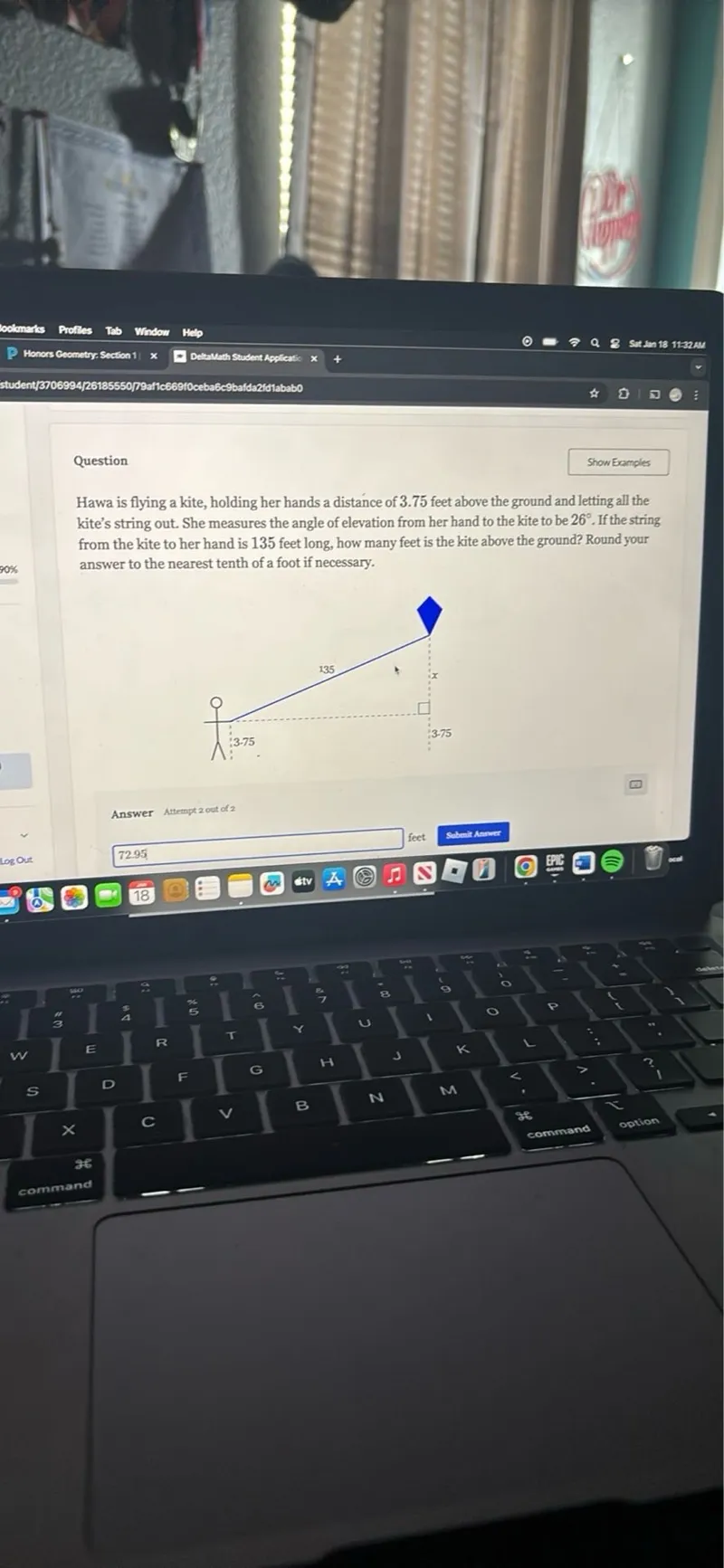
Transcript text: Hawa is flying a kite, holding her hands a distance of 3.75 feet above the ground and letting all the kite's string out. She measures the angle of elevation from her hand to the kite to be $26^{\circ}$. If the string from the kite to her hand is 135 feet long, how many feet is the kite above the ground? Round your answer to the nearest tenth of a foot if necessary.





