Questions: Identify the domain of the following function: f(x) = sqrt((x^2 - 8x)/4) (-8,0) (-∞,-8) ∪ (0, ∞) (0,8) (-∞, 0) ∪ (8, ∞)
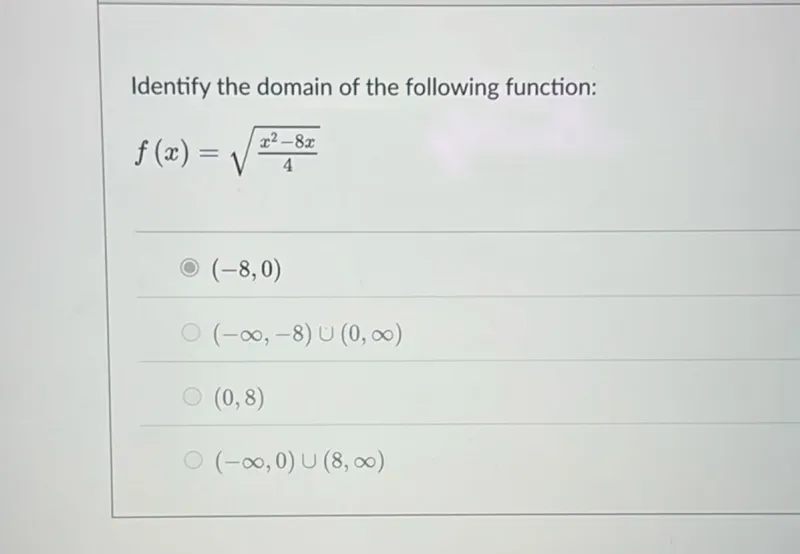
Transcript text: Identify the domain of the following function:
\[
f(x)=\sqrt{\frac{x^{2}-8 x}{4}}
\]
$(-8,0)$
$(-\infty,-8) \cup(0, \infty)$
$(0,8)$
$(-\infty, 0) \cup(8, \infty)$





