Questions: Find the distance between the two points in simplest radical form. (-5,-4) and (-2,-6)

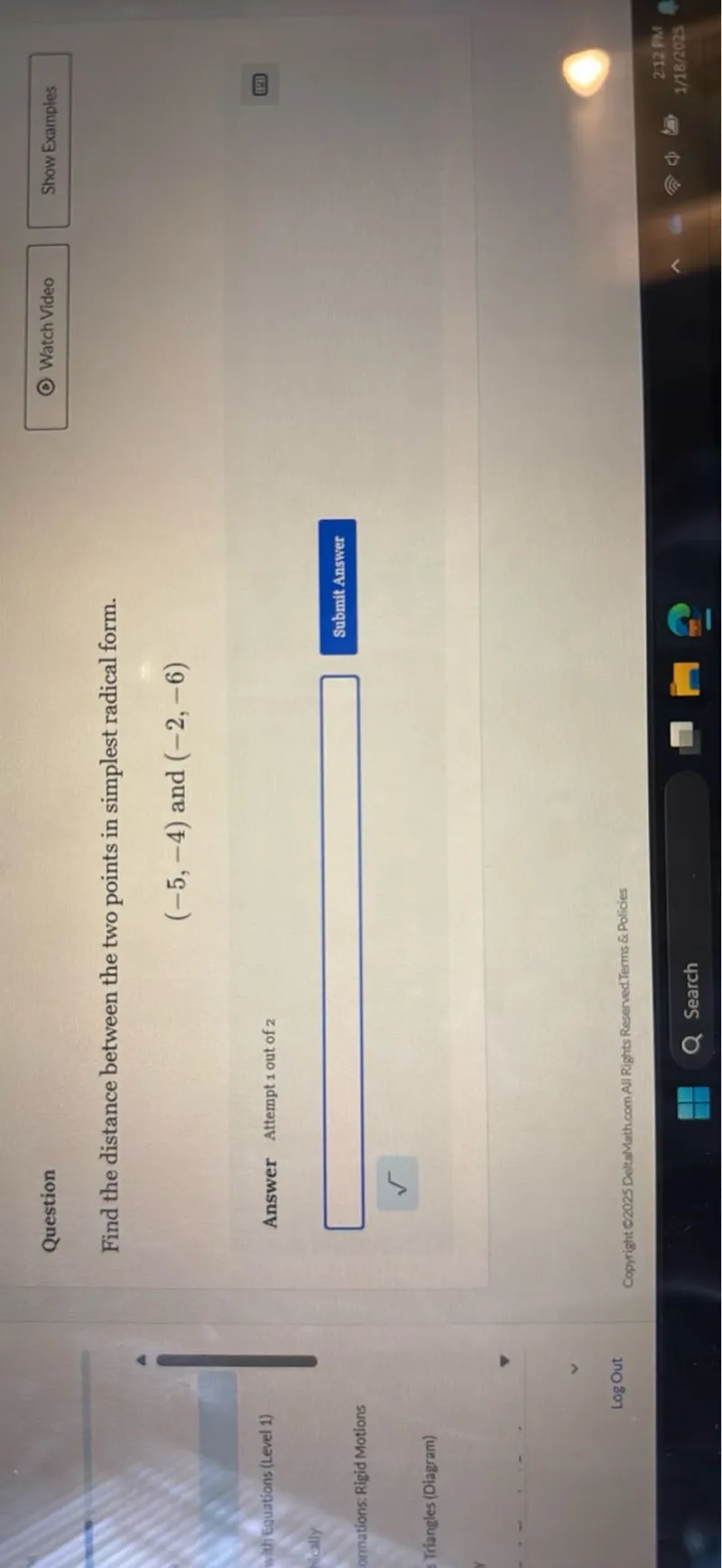
Transcript text: Find the distance between the two points in simplest radical form. \[ (-5,-4) \text { and }(-2,-6) \]

Solution

Step 1: Identify the coordinates

The coordinates of the two points are \((-5, -4)\) and \((-2, -6)\).

Step 2: Apply the distance formula

The distance \(d\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]

Step 3: Substitute the values into the formula

Substitute \(x_1 = -5\), \(y_1 = -4\), \(x_2 = -2\), and \(y_2 = -6\) into the formula: \[ d = \sqrt{(-2 - (-5))^2 + (-6 - (-4))^2} \]

Step 4: Simplify the expressions inside the square root

Calculate the differences: \[ d = \sqrt{(3)^2 + (-2)^2} \]

Step 5: Compute the squares

\[ d = \sqrt{9 + 4} \]

Step 6: Add the squared terms

\[ d = \sqrt{13} \]

\(\boxed{\sqrt{13}}\)

Was this solution helpful?

Unhelpful

Helpful

Thank you for your feedback.

Copied!