Questions: Describe the end behavior of f(x) = ln(x-4). What happens to the graph as x approaches infinity? As x approaches 4?

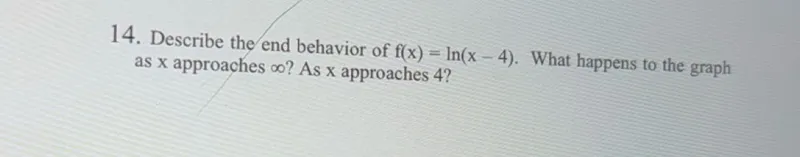
Transcript text: Describe the end behavior of $f(x)=\ln (x-4)$. What happens to the graph as $x$ approaches $\infty$ ? As $x$ approaches 4 ?

Solution

Solution Steps

Step 1: Analyze the behavior as $ x $ approaches $ \infty $

To determine the end behavior of $ f(x) = \ln(x-4) $ as $ x $ approaches $ \infty $, observe that the natural logarithm function $ \ln(y) $ grows without bound as $ y $ approaches $ \infty $. Here, $ y = x-4 $, so as $ x $ approaches $ \infty $, $ y $ also approaches $ \infty $. Therefore, $ f(x) = \ln(x-4) $ approaches $ \infty $.

Step 2: Analyze the behavior as $ x $ approaches 4

As $ x $ approaches 4 from the right ($ x \to 4^+ $), the expression $ x-4 $ approaches 0 from the positive side. The natural logarithm function $ \ln(y) $ approaches $ -\infty $ as $ y $ approaches 0 from the positive side. Therefore, $ f(x) = \ln(x-4) $ approaches $ -\infty $ as $ x $ approaches 4.

Step 3: Summarize the end behavior

As $ x $ approaches $ \infty $, $ f(x) = \ln(x-4) $ approaches $ \infty $.
As $ x $ approaches 4 from the right, $ f(x) = \ln(x-4) $ approaches $ -\infty $.