Questions: Solve the equation accurate to three decimal places. 3(8^(x-4)) = 38 Solve the equation accurate to three decimal places. (1 + 0.90/365)^(365t) = 2 Find the derivative of the function. y = 2^(-3x)
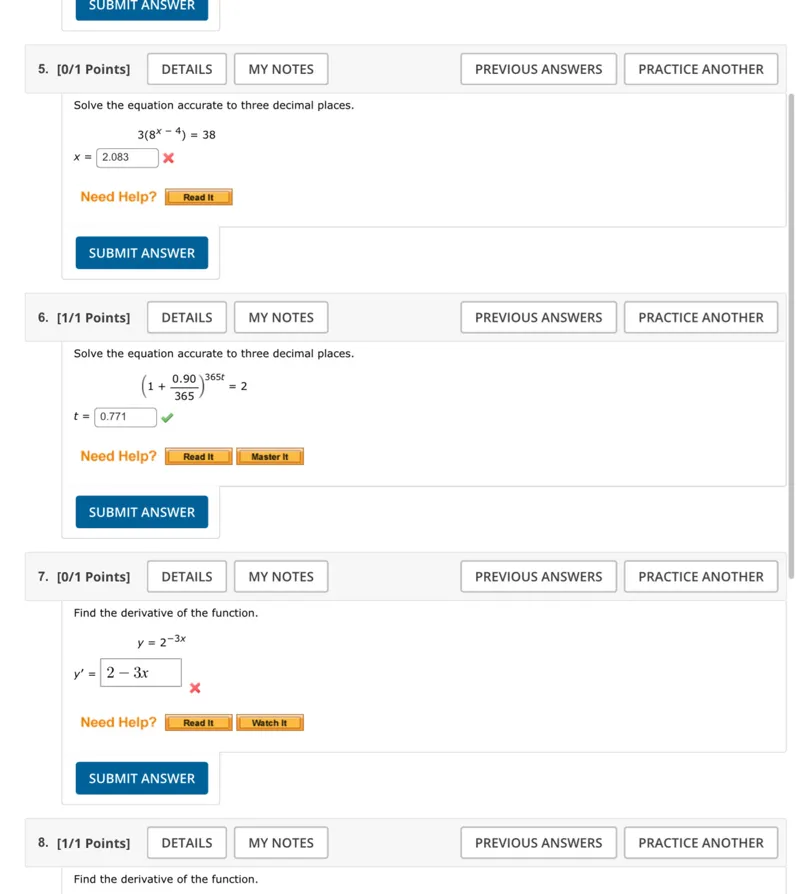
Transcript text: Solve the equation accurate to three decimal places.
\[ 3\left(8^{x-4}\right)=38 \]
Solve the equation accurate to three decimal places.
\[ \left(1+\frac{0.90}{365}\right)^{365 t}=2 \]
Find the derivative of the function.
\[ y=2^{-3 x} \]





