Questions: Problem 3 For the SOP equation: z=A̅ B C̅ + A̅ C D̅ + A̅ B C̅ D̅ + A B̅ C Use a K map to simplify this equation.
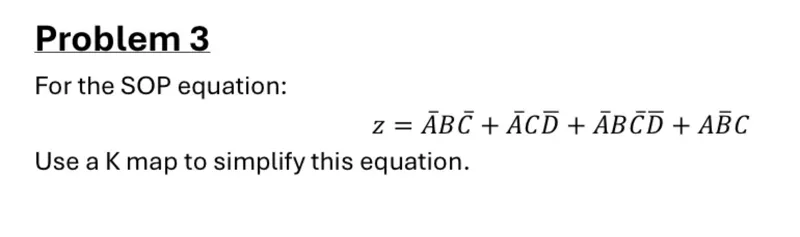
Transcript text: Problem 3
For the SOP equation:
\[
z=\bar{A} B \bar{C}+\bar{A} C \bar{D}+\bar{A} B \bar{C} \bar{D}+A \bar{B} C
\]
Use a K map to simplify this equation.





