Questions: Ten randomly selected cars were filled with either regular or premium gas (the decision was made based on a coin toss) and then driven on the freeway for the entirety of the tank of gas. The next day, each car was filled with whichever type of gas that was not used the previous day and then driven on the freeway for the entirety of the tank of gas. The mileage for each day was recorded and is summarized in the table below. MPG of 10 cars (regular/premium): 13/19, 20/22, 21/24, 23/25, 22/25, 27/26, 25/26, 27/28, 28/32, 22/24. Car 1 Car 2 Car 3 Car 4 Car 5 Car 6 Car 7 Car 8 Car 9 Car 10 Regular 16 20 21 23 22 27 25 27 28 22 Premium 19 22 24 25 25 26 26 28 32 24 You will be constructing a 90% confidence interval estimate of the difference between the mean efficiency of the car using regular and premium gas. You may assume that both samples are drawn from normally distributed populations. Question 1 Construct the 90% confidence interval estimate mean difference between the mileage from cars using regular and premium gas. Round your answer to 2 decimal places. < difference between the means <

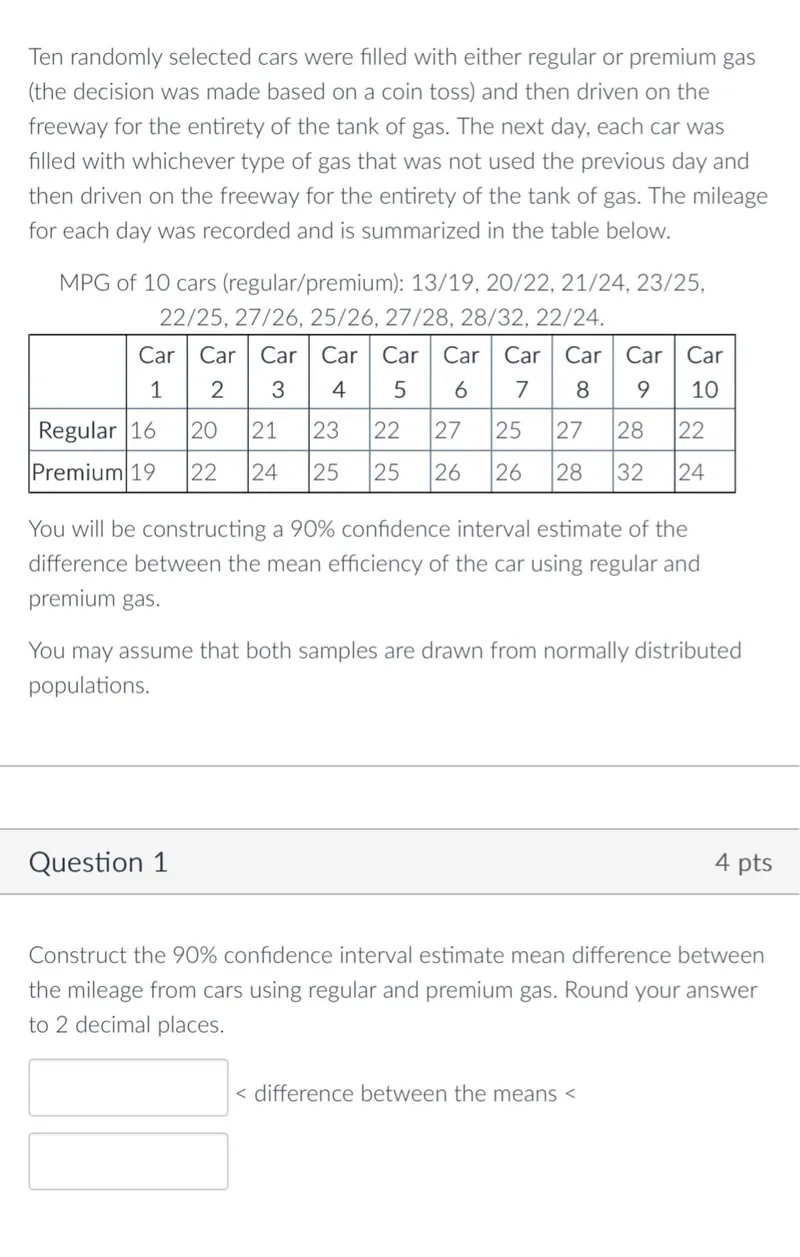
Ten randomly selected cars were filled with either regular or premium gas (the decision was made based on a coin toss) and then driven on the freeway for the entirety of the tank of gas. The next day, each car was filled with whichever type of gas that was not used the previous day and then driven on the freeway for the entirety of the tank of gas. The mileage for each day was recorded and is summarized in the table below. MPG of 10 cars (regular/premium): 13/19, 20/22, 21/24, 23/25, 22/25, 27/26, 25/26, 27/28, 28/32, 22/24. Car 1 Car 2 Car 3 Car 4 Car 5 Car 6 Car 7 Car 8 Car 9 Car 10 Regular 16 20 21 23 22 27 25 27 28 22 Premium 19 22 24 25 25 26 26 28 32 24 You will be constructing a 90% confidence interval estimate of the difference between the mean efficiency of the car using regular and premium gas. You may assume that both samples are drawn from normally distributed populations. Question 1 Construct the 90% confidence interval estimate mean difference between the mileage from cars using regular and premium gas. Round your answer to 2 decimal places. < difference between the means <
Transcript text: Ten randomly selected cars were filled with either regular or premium gas (the decision was made based on a coin toss) and then driven on the freeway for the entirety of the tank of gas. The next day, each car was filled with whichever type of gas that was not used the previous day and then driven on the freeway for the entirety of the tank of gas. The mileage for each day was recorded and is summarized in the table below. MPG of 10 cars (regular/premium): 13/19, 20/22, 21/24, 23/25, 22/25, 27/26, 25/26, 27/28, 28/32, 22/24. \begin{tabular}{|l|c|c|c|c|c|c|c|c|c|c|} \hline & Car & Car & Car & Car & Car & Car & Car & Car & Car & Car \\ & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline Regular & 16 & 20 & 21 & 23 & 22 & 27 & 25 & 27 & 28 & 22 \\ \hline Premium & 19 & 22 & 24 & 25 & 25 & 26 & 26 & 28 & 32 & 24 \\ \hline \end{tabular} You will be constructing a 90\% confidence interval estimate of the difference between the mean efficiency of the car using regular and premium gas. You may assume that both samples are drawn from normally distributed populations. Question 1 4 pts Construct the $90 \%$ confidence interval estimate mean difference between the mileage from cars using regular and premium gas. Round your answer to 2 decimal places. $\square$ < difference between the means < $\square$
failed

Solution

failed
failed

Solution Steps

Step 1: Calculate the Standard Error

The standard error (SE) is calculated using the formula: \[ SE = \frac{s}{\sqrt{n}} = \frac{1.41}{\sqrt{10}} = 0.45 \]

Step 2: Calculate the Test Statistic

The test statistic \( t \) is calculated using the formula: \[ t = \frac{\bar{d}}{SE} = \frac{-2.0}{0.45} = -4.47 \]

Step 3: Determine the Critical Value

For a two-tailed test at \( \alpha = 0.1 \), the critical value is: \[ t_{\alpha/2, df} = t_{(0.05, 9)} = 1.83 \]

Step 4: Calculate the P-value

The P-value is calculated as: \[ P = 2 \times (1 - T(|t|)) = 2 \times (1 - T(4.47)) = 0.0 \]

Step 5: Calculate the Confidence Interval

The 90% confidence interval for the difference between the means is calculated as: \[ \text{Lower limit} = \bar{d} - t_{\alpha/2} \cdot SE = -2.0 - 1.83 \cdot 0.45 = -2.8235 \] \[ \text{Upper limit} = \bar{d} + t_{\alpha/2} \cdot SE = -2.0 + 1.83 \cdot 0.45 = -1.1765 \]

Step 6: Present the Confidence Interval

The final 90% confidence interval for the difference between the means is: \[ -2.8235 < \text{difference between the means} < -1.1765 \]

Final Answer

\( -2.82 < \text{difference between the means} < -1.18 \)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
How many square decimeters are in 510 m²?
failedAnswered
Suppose L and M are not mutually exclusive events with P(L)=0.45, P(M)=0.55, P(L and M)=0.2. Find P(L or M).
failedAnswered
Déterminer si les matrices suivantes sont idempotentes. a) A=[0 1; 0 1] b) B=[2 -1; 2 4] c) C=[-11 4; -33 12] d) E=[1 0 0; 0 1 1; 0 -1 1]
failedAnswered
Consider the reaction below which has a ΔG=+0.5 kJ/mol: A+B ⇌ C+D 10 M A, 10 M B, 1 M C and 1 M D are added to a container at room temperature. Which of the following statements is TRUE? To reach equilibrium, the reaction will proceed in the forward direction. To reach equilibrium, the reaction will proceed alternating between forward and reverse direction. To reach equilibrium, the reaction will proceed in the reverse direction. To reach equilibrium, the reaction will NOT proceed in either direction.
failedAnswered
Multiple Choice Question Which of the following is correct regarding the scope of operations management? Operations management involves acquiring resources and converting raw material into outputs using one or more transformation processe One of the primary functions of operations management is strategy interpretation and communication. Operations management is not involved in higher-level decision making. Need help? Review these concept resources. (7) Read About the Concept