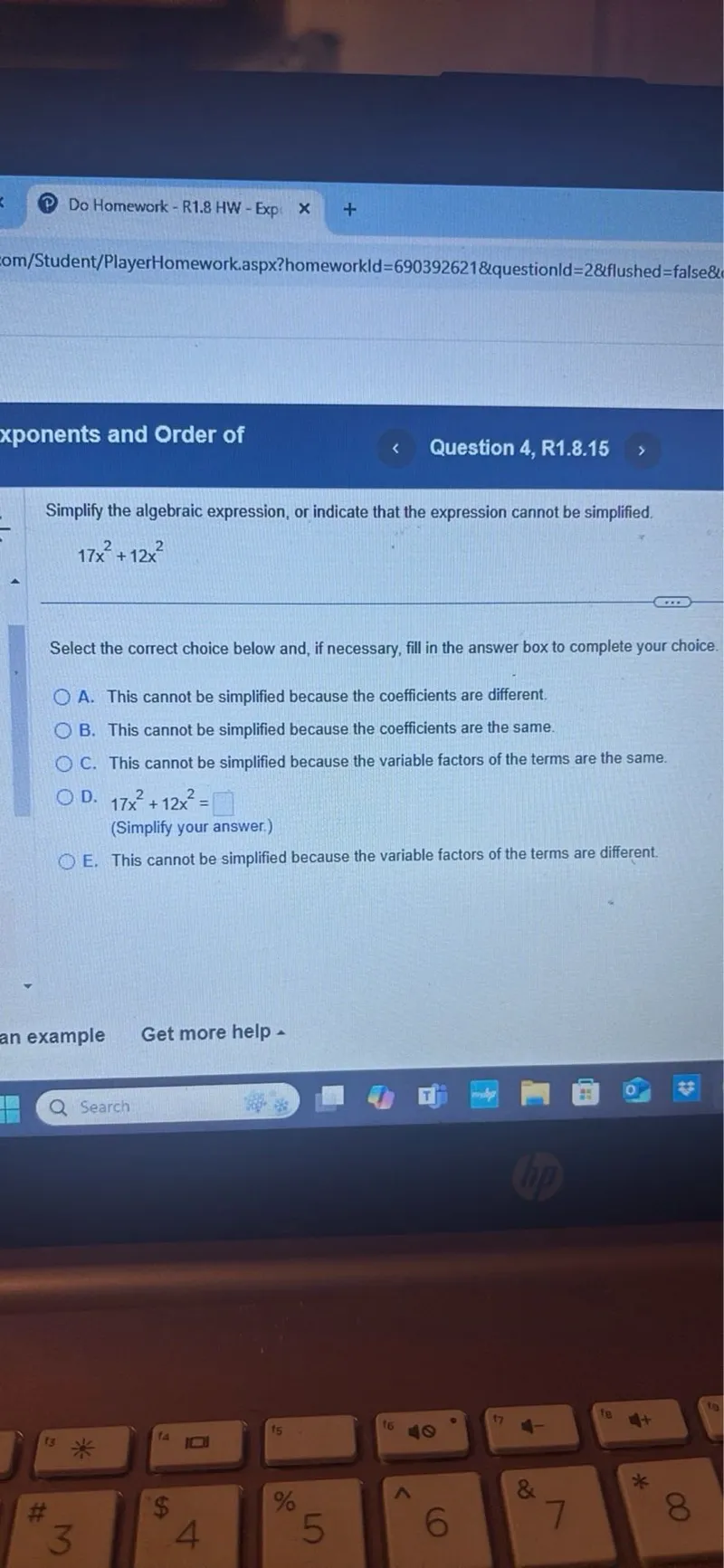
Questions: Do Homework - R1.8 HW - Exponents and Order of Question 4, R1.8.15 Simplify the algebraic expression, or indicate that the expression cannot be simplified. 17 x^2 + 12 x^2 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. This cannot be simplified because the coefficients are different. B. This cannot be simplified because the coefficients are the same. C. This cannot be simplified because the variable factors of the terms are the same. D. 17 x^2 + 12 x^2 = □ (Simplify your answer.) E. This cannot be simplified because the variable factors of the terms are different.

Do Homework - R1.8 HW - Exponents and Order of Question 4, R1.8.15 Simplify the algebraic expression, or indicate that the expression cannot be simplified. 17 x^2 + 12 x^2 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. This cannot be simplified because the coefficients are different. B. This cannot be simplified because the coefficients are the same. C. This cannot be simplified because the variable factors of the terms are the same. D. 17 x^2 + 12 x^2 = □ (Simplify your answer.) E. This cannot be simplified because the variable factors of the terms are different.
Transcript text: Do Homework - R1.8 HW - Exp om/Student/PlayerHomework.aspx?homeworkld=690392621\&questionld=2\&flushed=false\& xponents and Order of Question 4, R1.8.15 Simplify the algebraic expression, or indicate that the expression cannot be simplified. \[ 17 x^{2}+12 x^{2} \] Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. This cannot be simplified because the coefficients are different. B. This cannot be simplified because the coefficients are the same. C. This cannot be simplified because the variable factors of the terms are the same. D. $17 x^{2}+12 x^{2}=$ $\square$ (Simplify your answer.) E. This cannot be simplified because the variable factors of the terms are different. an example Get more help - Search
failed

Solution

failed
failed

Solution Steps

Step 1: Identify Like Terms

The expression \(17x^{2} + 12x^{2}\) contains two terms with the same variable factor \(x^{2}\). These are called like terms.

Step 2: Combine Like Terms

Since the terms have the same variable factor, their coefficients can be added together: \[ 17x^{2} + 12x^{2} = (17 + 12)x^{2} \]

Step 3: Simplify the Coefficients

Add the coefficients \(17\) and \(12\): \[ 17 + 12 = 29 \] Thus, the simplified expression is: \[ 29x^{2} \]

Step 4: Select the Correct Choice

The correct choice is: D. \(17x^{2} + 12x^{2} =\) \(\boxed{29x^{2}}\)

Final Answer

D. \(17x^{2} + 12x^{2} = \boxed{29x^{2}}\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Which scientist presented arguments to support a theory of geological change, proposing that the earth was subject to slow but continuous erosion and uplift?
failedAnswered
Multiply the polynomials using the distributive property and combine like terms. (-x-6)(2x-1)
failedAnswered
Example 4 Abdulla invests some money into an account for 3 years and receives 612 QR in interest. Saeed invests 700 QR more than Abdulla at the same interest rate for 2 years and gets 492 QAR in interest. How much did Abdulla invest in the account? NOTE: I=PRT, rearrange the formula to solve for R. Make the rates equal to each other. P= initial amount invested, I= interest amount, and T= time in years
failedAnswered
Use the sample data below to answer the following question(s). Use a 0.05 significance level and the observed frequencies of 144 drownings at the beaches of a randomly selected coastal state to test the claim that the number of drownings for each month is equally likely. Jan Feb Mar Apr May June July Aug Sept Oct Nov Dec 1 3 2 7 14 20 37 33 16 6 2 3 Determine the value of the χ^2 test statistic.
failedAnswered
You are the payroll manager for a women's apparel company. Your workers are paid per garment sewn on a differential piecework schedule as follows. Pay Level Garments Produced Rate per Garment 1 1-50 4.60 2 51-100 5.25 3 101-150 5.50 4 Over 150 6.10 Calculate last week's total gross pay (in ) for employee "Goodrich, P." who produced 103 garments.