Questions: How many significant figures should the answer in each of these calculations contain? (a) (93.9)(8.8) significant figures(s) (b) (0.3506)(8.2) significant figures(s) (c) (550)(91)/2 significant figures(s) (d) 3.9+0.562 significant figures(s) (e) 31.0/3.8 significant figure(s) (f) 1,700+5.16 significant figures(s) (g) 9.8+39-0.007 significant figures(s)

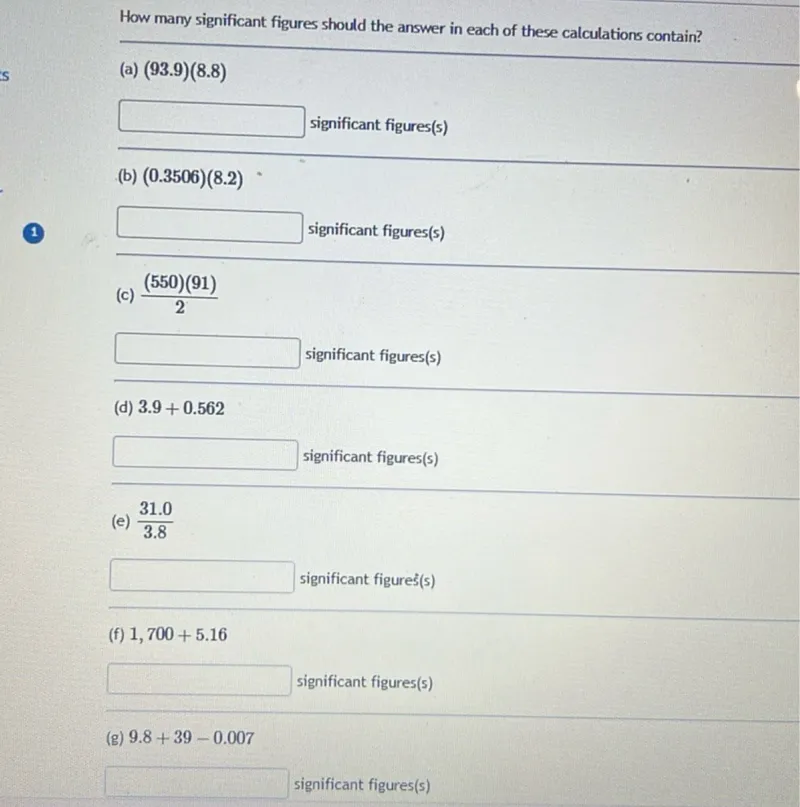
How many significant figures should the answer in each of these calculations contain? (a) (93.9)(8.8) significant figures(s) (b) (0.3506)(8.2) significant figures(s) (c) (550)(91)/2 significant figures(s) (d) 3.9+0.562 significant figures(s) (e) 31.0/3.8 significant figure(s) (f) 1,700+5.16 significant figures(s) (g) 9.8+39-0.007 significant figures(s)
Transcript text: How many significant figures should the answer in each of these calculations contain? (a) $(93.9)(8.8)$ $\square$ significant figures(s) (b) $(0.3506)(8.2)$ $\square$ significant figures(s) (c) $\frac{(550)(91)}{2}$ $\square$ significant figures(s) (d) $3.9+0.562$ $\square$ significant figures(s) (e) $\frac{31.0}{3.8}$ $\square$ significant figureś(s) (f) $1,700+5.16$ $\square$ significant figures(s) (g) $9.8+39-0.007$ $\square$ significant figures(s)
failed

Solution

failed
failed

Solution Steps

Step 1: Determine Significant Figures for Multiplication and Division
  • For multiplication and division, the number of significant figures in the result should be the same as the number in the least precise measurement used in the calculation.
Step 2: Apply Rule to Part (a)
  • \( (93.9)(8.8) \)
  • 93.9 has 3 significant figures, and 8.8 has 2 significant figures.
  • The result should have 2 significant figures.
Step 3: Apply Rule to Part (b)
  • \( (0.3506)(8.2) \)
  • 0.3506 has 4 significant figures, and 8.2 has 2 significant figures.
  • The result should have 2 significant figures.
Step 4: Apply Rule to Part (c)
  • \( \frac{(550)(91)}{2} \)
  • 550 has 2 significant figures, 91 has 2 significant figures, and 2 is an exact number (infinite significant figures).
  • The result should have 2 significant figures.
Step 5: Determine Significant Figures for Addition and Subtraction
  • For addition and subtraction, the number of decimal places in the result should be the same as the number in the least precise measurement used in the calculation.
Step 6: Apply Rule to Part (d)
  • \( 3.9 + 0.562 \)
  • 3.9 has 1 decimal place, and 0.562 has 3 decimal places.
  • The result should have 1 decimal place.
Step 7: Apply Rule to Part (e)
  • \( \frac{31.0}{3.8} \)
  • 31.0 has 3 significant figures, and 3.8 has 2 significant figures.
  • The result should have 2 significant figures.
Step 8: Apply Rule to Part (f)
  • \( 1,700 + 5.16 \)
  • 1,700 is ambiguous in terms of significant figures (could be 2, 3, or 4), but typically treated as 2 significant figures if not specified.
  • 5.16 has 2 decimal places.
  • The result should be rounded to the nearest ten, assuming 1,700 has 2 significant figures.
Step 9: Apply Rule to Part (g)
  • \( 9.8 + 39 - 0.007 \)
  • 9.8 has 1 decimal place, 39 has no decimal places, and 0.007 has 3 decimal places.
  • The result should have no decimal places.

Final Answer

(a) \(\boxed{2}\) significant figures(s)
(b) \(\boxed{2}\) significant figures(s)
(c) \(\boxed{2}\) significant figures(s)
(d) \(\boxed{1}\) significant figures(s)
(e) \(\boxed{2}\) significant figures(s)
(f) \(\boxed{2}\) significant figures(s)
(g) \(\boxed{0}\) significant figures(s)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Solve each equation. Remember to check for extraneous solutions. 2) sqrt(2x+10) = x+5 Identify your a, h, k. Then sketch the graph.
failedAnswered
Submitting an external tool Question Consider the reaction described by the following chemical equation. 2 Ag2 S(s)+2 H2 O(l) -> 4 Ag(s)+2 H2 S(g)+O2(g) ΔHrxn^°=595.5 kJ/mol The change in enthalpy for this reaction can be determined theoretically by using the standard enthalpies of formation for the species involved. ΔHrxn^°=∑ n ΔHf products^°-∑ n ΔHf reactants^° What is the value for the standard enthalpy of formation for Ag(s) that would be used in the equation above? Provide your answer below: kJ / mol
failedAnswered
A bullet with mass 15 g is traveling at 350 m / s when it strikes a stationary wooden object with mass 500 g. The bullet emerges on the other side of the object but has slowed to 75 m / s. What is the kinetic energy of the wooden object?
failedAnswered
Plot two points on the boundary line of the graph of the line x, y=1, 1
failedAnswered
What is the function of casein in milk?