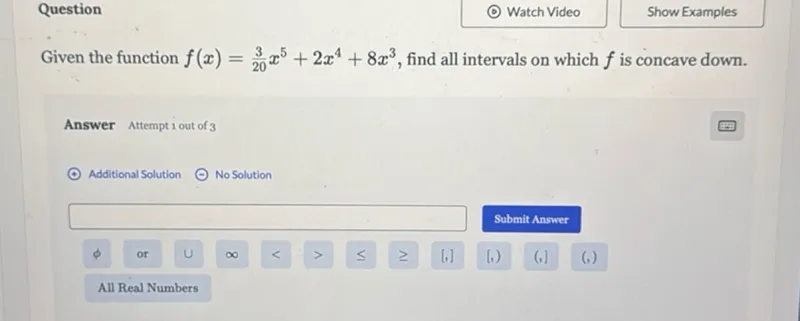
Find the intervals where the function \( f(x) = \frac{3}{20}x^5 + 2x^4 + 8x^3 \) is concave down.
Calculate the first derivative, \( f'(x) \).
The first derivative is calculated as follows:
\[ f'(x) = \frac{3}{20} \cdot 5x^4 + 2 \cdot 4x^3 + 8 \cdot 3x^2 = \frac{3}{4}x^4 + 8x^3 + 24x^2 \]
Calculate the second derivative, \( f''(x) \).
The second derivative is calculated as follows:
\[ f''(x) = \frac{3}{4} \cdot 4x^3 + 8 \cdot 3x^2 + 24 \cdot 2x = 3x^3 + 24x^2 + 48x \]
Find the critical points of \( f''(x) \) by setting \( f''(x) = 0 \) and solving for \( x \).
Set the second derivative to zero and solve:
\[ 3x^3 + 24x^2 + 48x = 0 \]
\[ 3x(x^2 + 8x + 16) = 0 \]
\[ 3x(x + 4)^2 = 0 \]
The critical points are \( x = 0 \) and \( x = -4 \).
Create a sign chart for \( f''(x) \) using the critical points.
Evaluate the sign of \( f''(x) = 3x(x+4)^2 \) in each interval:
For \( x < -4 \), test \( x = -5 \):
\[ 3(-5)(-5+4)^2 = -15 \] (negative)
For \( -4 < x < 0 \), test \( x = -1 \):
\[ 3(-1)(-1+4)^2 = -27 \] (negative)
For \( x > 0 \), test \( x = 1 \):
\[ 3(1)(1+4)^2 = 75 \] (positive)
Identify the intervals where \( f''(x) < 0 \).
From the sign chart, \( f''(x) < 0 \) when \( x < 0 \), except for \( x = -4 \) where \( f''(x) = 0 \). Therefore, the function is concave down on the interval \( (-\infty, 0) \).
\(\boxed{(-\infty, 0)}\)
The function \( f(x) = \frac{3}{20}x^5 + 2x^4 + 8x^3 \) is concave down on the interval \((-∞, 0)\).