Questions: Assuming a conservative interest rate of 4.2%, how much would you need to save each year to reach 85,000 in 14 years? Round to the nearest 100.
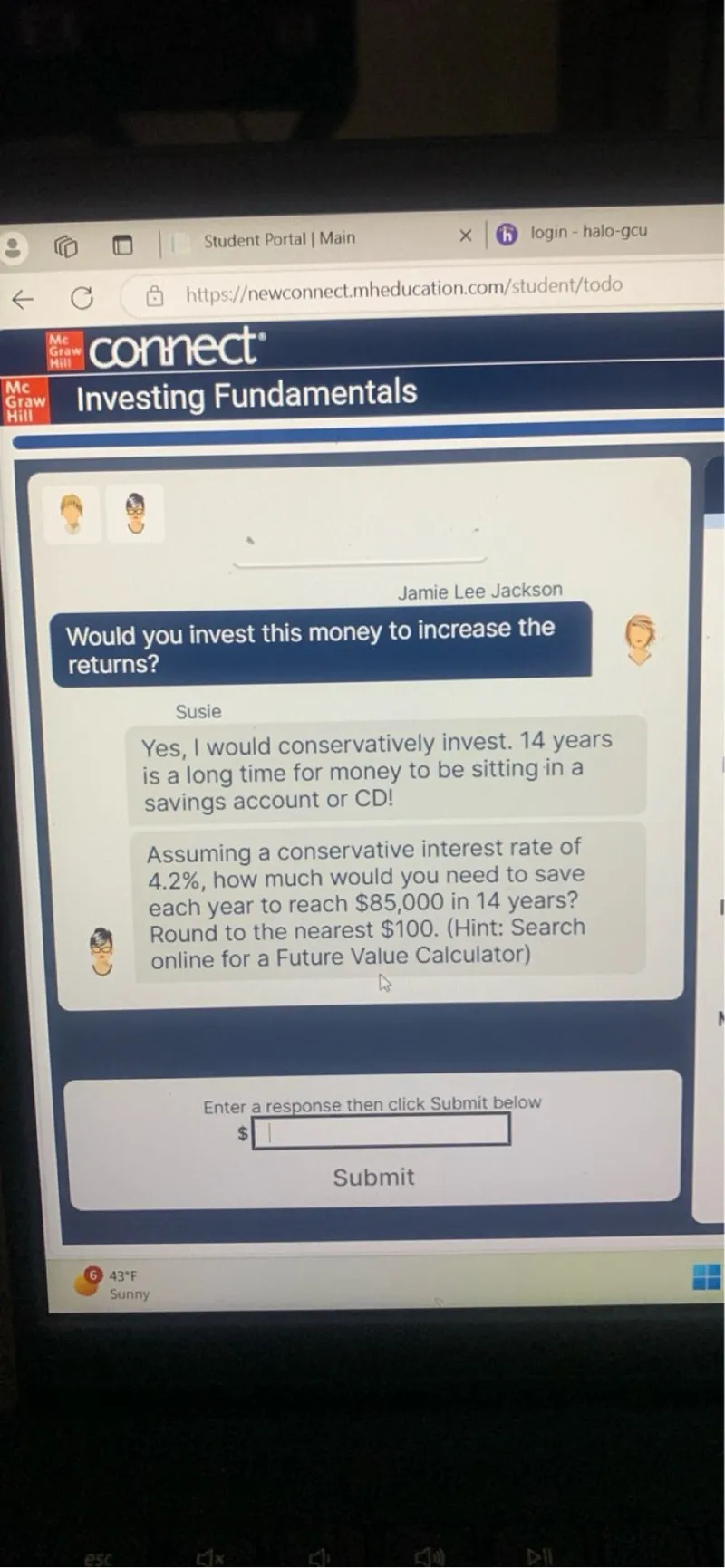
Transcript text: Assuming a conservative interest rate of $4.2 \%$, how much would you need to save each year to reach $\$ 85,000$ in 14 years? Round to the nearest $\$ 100$.





