Questions: In a survey of women in the United States (ages 20-29), the mean height was 64.1 inches with a population standard deviation of 2.71 inches. Women's heights are normally distributed. a) What height represents the 95th percentile? b) What height represents the first quartile?
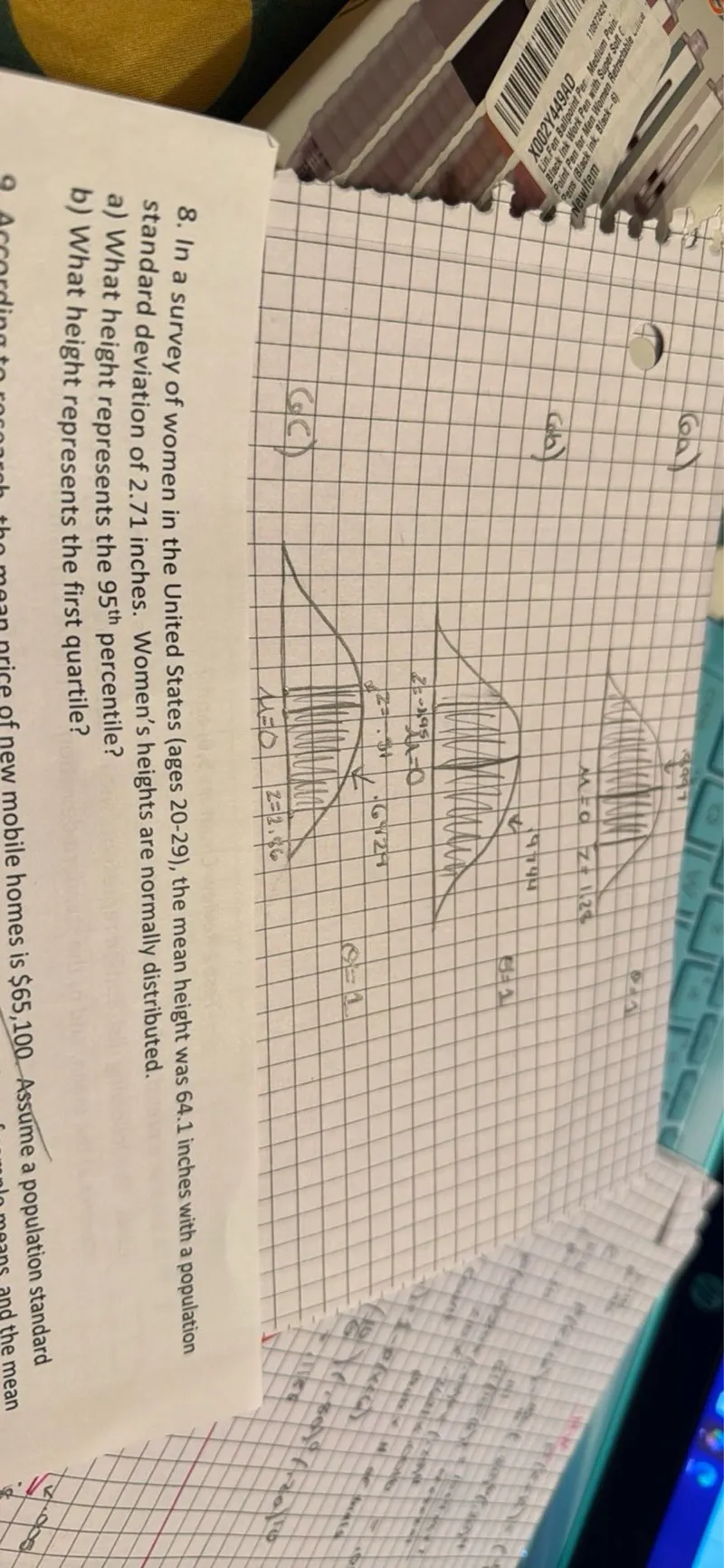
Transcript text: In a survey of women in the United States (ages 20-29), the mean height was 64.1 inches with a population standard deviation of 2.71 inches. Women's heights are normally distributed.
a) What height represents the $95^{\text {th }}$ percentile?
b) What height represents the first quartile?





