Questions: (a) Find the following side lengths for the net. A=7 mm B=10 mm C=4 mm D=4 mm (b) Use the net to find the surface area of the prism. mm^2
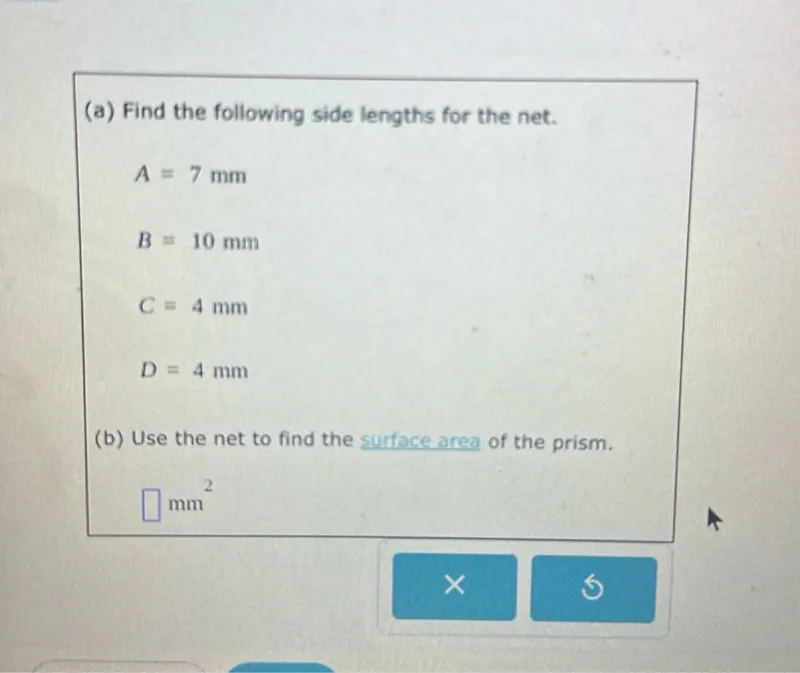
Transcript text: (a) Find the following side lengths for the net.
\[
A=7 \mathrm{~mm}
\]
\[
B=10 \mathrm{~mm}
\]
\[
C=4 \mathrm{~mm}
\]
\[
D=4 \mathrm{~mm}
\]
(b) Use the net to find the surface area of the prism.
$\square$ $\mathrm{mm}^{2}$





