Questions: Algebra 2 Sem1 Quiz 2.2.1 - Factoring Factor completely: 9 x^2 + 12 x + 4 a. (2 x + 3)^2 b. (3 x + 2)^2 c. (3 x + 2)(3 x - 2) d. (2 x + 3)(3 x + 2)
Transcript text: Algebra 2 Sem1
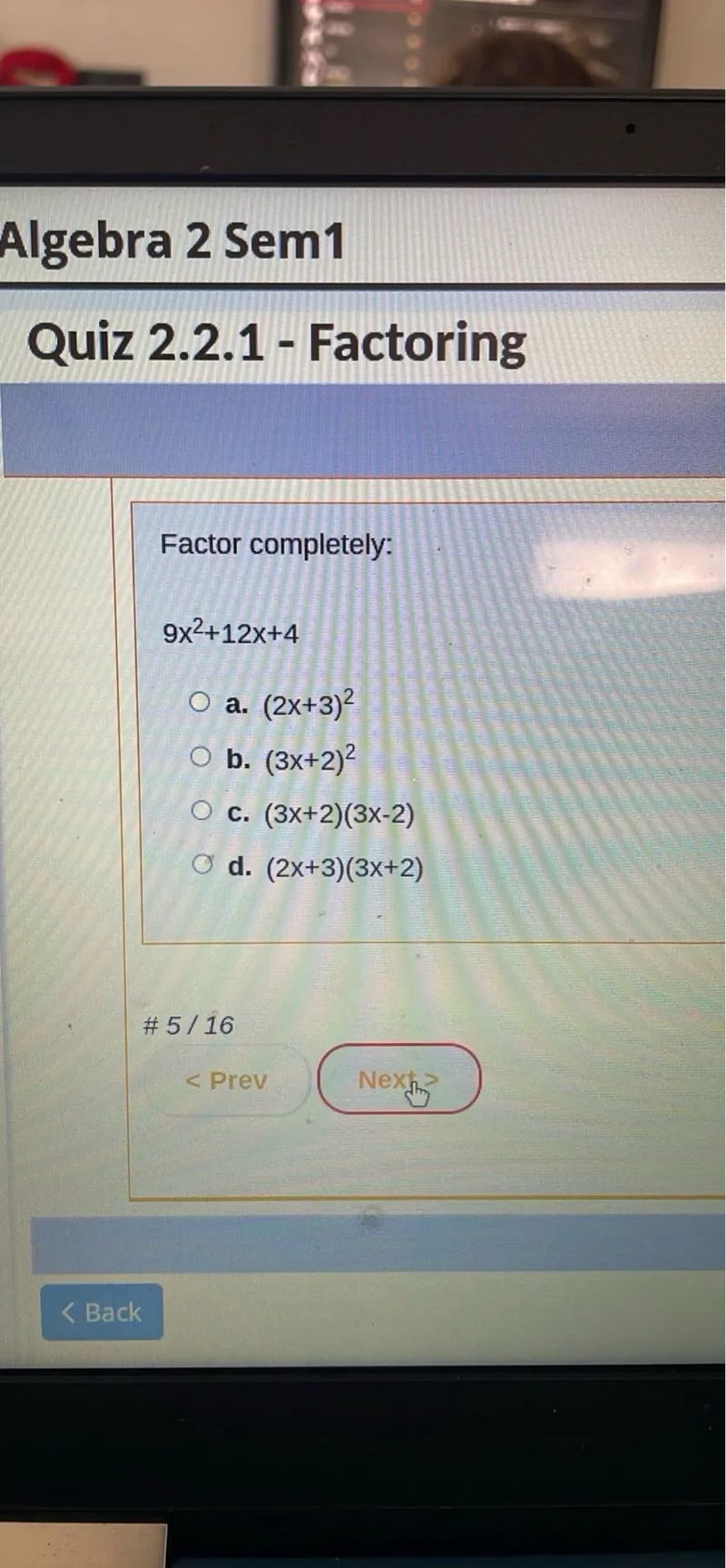
Quiz 2.2.1 - Factoring
Factor completely:
\[
9 x^{2}+12 x+4
\]
a. $(2 x+3)^{2}$
b. $(3 x+2)^{2}$
c. $(3 x+2)(3 x-2)$
d. $(2 x+3)(3 x+2)$





