Questions: Fill in the missing values to make the equations true. (a) log2 11 + log2 5 = log2 □ (b) log3 □ - log3 4 = log3 7/4 (c) log9 32 = □ log9 2
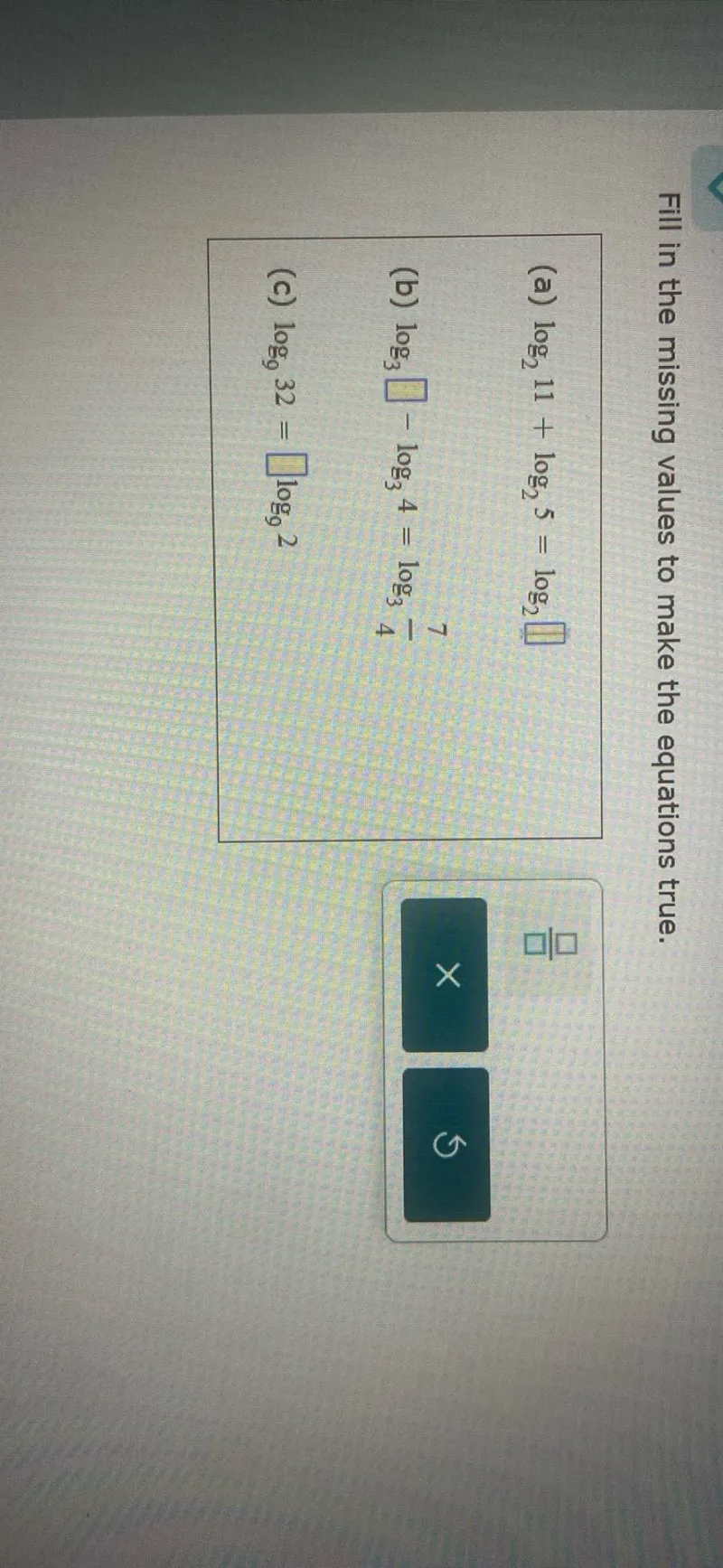
Transcript text: Fill in the missing values to make the equations true.
(a) $\log _{2} 11+\log _{2} 5=\log _{2}$ $\square$
(b) $\log _{3}$ $\square$ $-\log _{3} 4=\log _{3} \frac{7}{4}$
(c) $\log _{9} 32=$ $\square$ $\log _{9} 2$





