Questions: A sample of 400 people is classified according to highest educational degree earned ("no college degree", "Two-year degree", "Four-year degree", "Advanced degree") and according to place of residence ("urban", "Suburban", or "rural"). They are also classified and given in the contingency table below. No college degree Two-year degree Four-year degree Advanced degree Urban 34 48 19 33 Suburban 30 49 15 49 Rural 16 44 39 24 Among the people in the sample who have an advanced degree, what is the relative frequency of those whose place of residence happens to be urban? Round your answer to two decimal places.

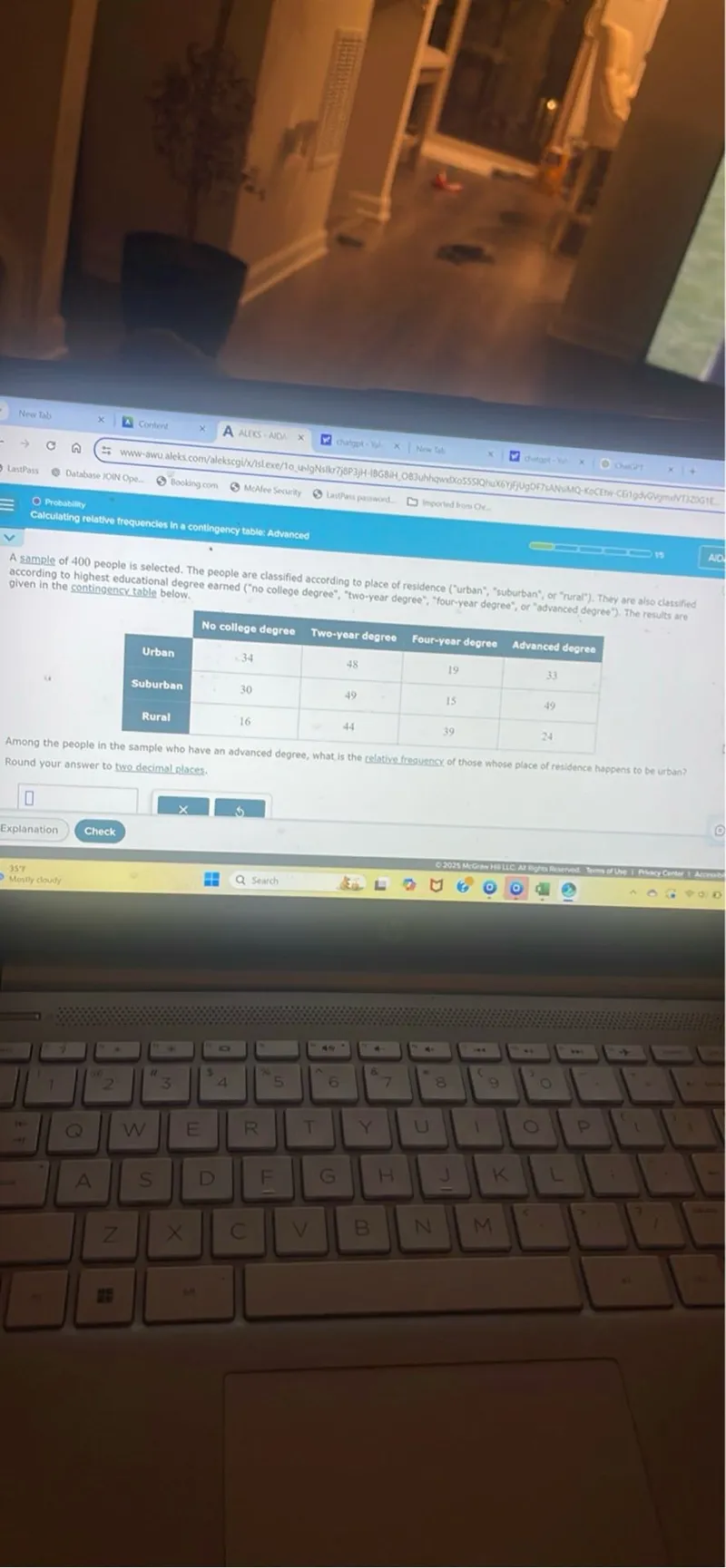
A sample of 400 people is classified according to highest educational degree earned ("no college degree", "Two-year degree", "Four-year degree", "Advanced degree") and according to place of residence ("urban", "Suburban", or "rural"). They are also classified and given in the contingency table below. No college degree Two-year degree Four-year degree Advanced degree Urban 34 48 19 33 Suburban 30 49 15 49 Rural 16 44 39 24 Among the people in the sample who have an advanced degree, what is the relative frequency of those whose place of residence happens to be urban? Round your answer to two decimal places.
Transcript text: A sample of 400 people is classified according to highest educational degree earned ("no college degree", "Two-year degree", "Four-year degree", "Advanced degree") and according to place of residence ("urban", "Suburban", or "rural"). They are also classified and given in the contingency table below. \begin{tabular}{|c|c|c|c|c|} \cline { 2 - 5 } \multicolumn{1}{c|}{} & No college degree & Two-year degree & Four-year degree & Advanced degree \\ \hline Urban & 34 & 48 & 19 & 33 \\ \hline Suburban & 30 & 49 & 15 & 49 \\ \hline Rural & 16 & 44 & 39 & 24 \\ \hline \end{tabular} Among the people in the sample who have an advanced degree, what is the relative frequency of those whose place of residence happens to be urban? Round your answer to two decimal places.
failed

Solution

failed
failed

Solution Steps

Step 1: Identify the Target Group

The target group is defined by specific criteria within the sample. For this calculation, the size of the target group (T) has been identified based on the given criteria.

Step 2: Calculate the Size of the Target Group (T)

The size of the target group is given as 33.

Step 3: Calculate the Total Sample Size (N)

The total sample size is given as 106.

Step 4: Calculate Relative Frequency

Using the formula \(\text{Relative Frequency} = \frac{T}{N}\), where \(T\) is the size of the target group and \(N\) is the total sample size, we calculate the relative frequency. \(\text{Relative Frequency} = \frac{33}{106} = 0.31\)

Final Answer

The relative frequency of the target group within the sample, rounded to 2 decimal places, is 0.31.

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
What is true about nonmaterial culture and material culture? (Select all that apply) Material culture is tangible and nonmaterial culture is intangible. Nonmaterial culture includes ideas, attitudes, and beliefs. Material culture includes clothing, books, and tools.
failedAnswered
Question 4 (1 point) (16.4) The IUPAC name and the common name for the following ester are methyl ethanoate; methyl acetate methyl methanoate; methyl acetate methyl methanoate; methyl formate methyl ethanoate: methyl formate
failedAnswered
Use the given graph of the function y=f(x) to find the following quantities, if they exist. (If an answer does not exist, enter DNE.) (a) lim x -> 2 f(x) (b) lim x -> 5- f(x) (c) lim x -> 5+ f(x)
failedAnswered
2 Multiple Choice 1 point Which of the following structures conencts the third ventricle to the fourth ventricle? Cerebral aqueduct Choriod plexus Interventricular foramen Falx cerebri
failedAnswered
Abdominal fat is considered a greater threat to health than fat in the hips and thighs because abdominal fat Multiple Choice reduces lung capacity. squeezes the heart. more easily enters the bloodstream. causes lower back ailments that lead to inactivity.