Questions: Write an equation of the function whose graph is shown in the figure below. y=-4 cos (π/5 x)-3 y=4 sin (π/5 x)-3 y=4 cos (π/5 x)+3 y=-4 sin (π/2 x)+3
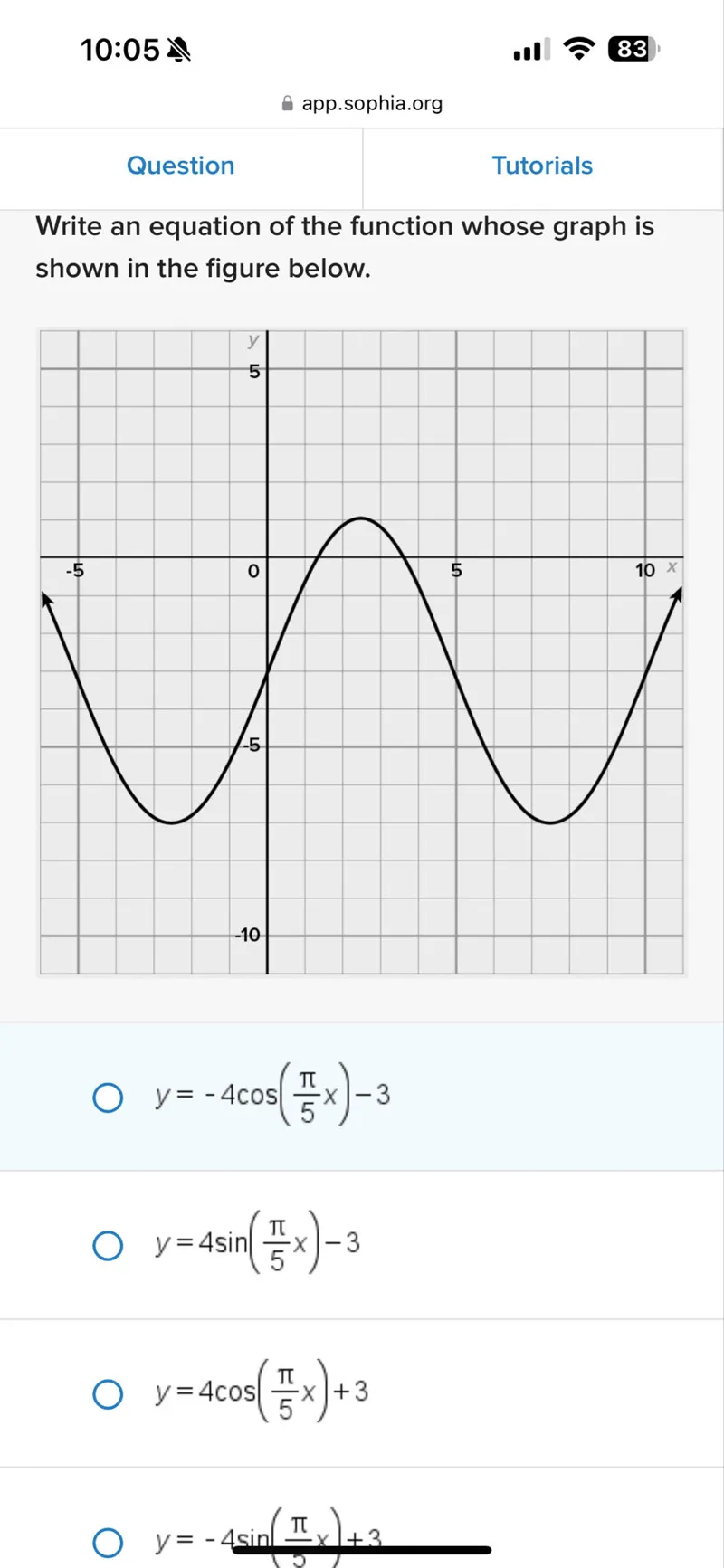
Transcript text: Write an equation of the function whose graph is shown in the figure below.
$y=-4 \cos \left(\frac{\pi}{5} x\right)-3$
$y=4 \sin \left(\frac{\pi}{5} x\right)-3$
$y=4 \cos \left(\frac{\pi}{5} x\right)+3$
$y=-4 \sin \left(\frac{\pi}{2} x\right)+3$





