Questions: Find the equation of the line tangent to the given curve at (x=a). Use a graphing utility to graph the curve and the tangent line on the same set of axes. (y=frac5 xx-3 ; a=4) The equation for the tangent line is (y=) (Type an expression using x as the variable.)
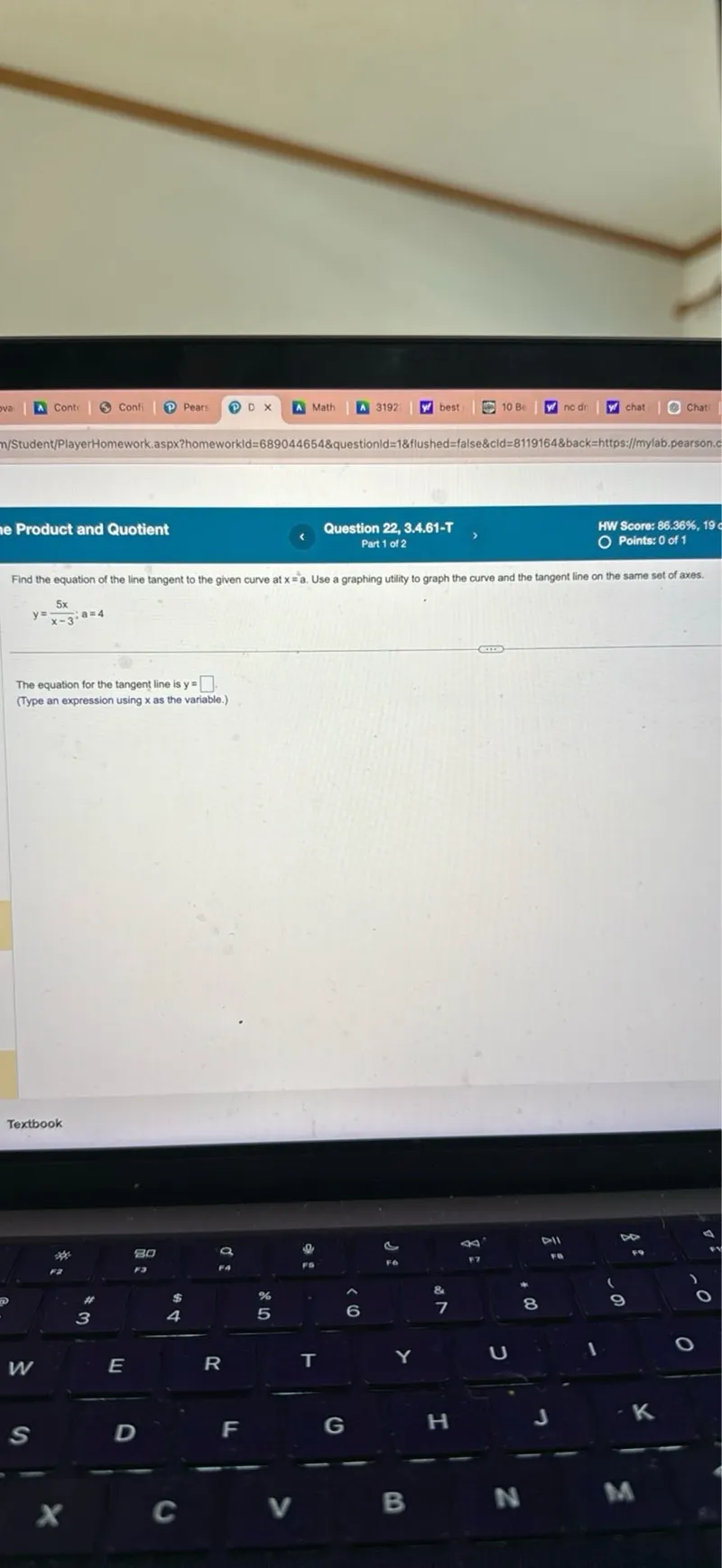
Transcript text: Find the equation of the line tangent to the given curve at $x=a$. Use a graphing utility to graph the curve and the tangent line on the same set of axes.
\[
y=\frac{5 x}{x-3} ; a=4
\]
The equation for the tangent line is $y=$ $\square$
(Type an expression using x as the variable.)





