Questions: The gusset plate is subjected to the forces of four members. Determine the force in member B and its proper orientation θ for equilibrium. The forces are concurrent at point O. Take F = 12 kN.

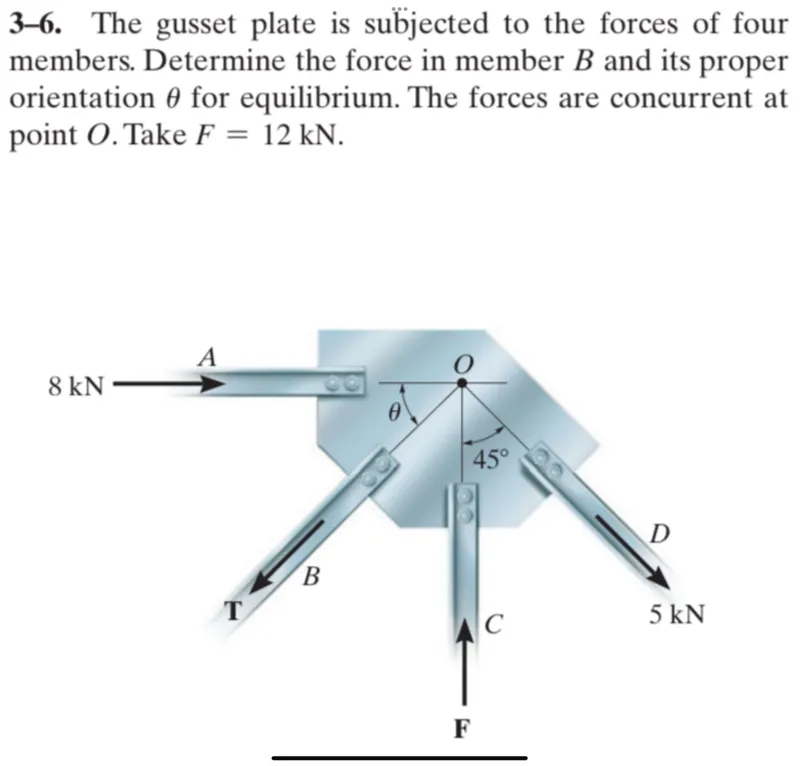
The gusset plate is subjected to the forces of four members. Determine the force in member B and its proper orientation θ for equilibrium. The forces are concurrent at point O. Take F = 12 kN.

Transcript text: The gusset plate is subjected to the forces of four members. Determine the force in member $B$ and its proper orientation $\theta$ for equilibrium. The forces are concurrent at point $O$. Take $F=12 \mathrm{kN}$.

Solution

Solution Steps

Step 1: Define the coordinate system and forces

Let's set up a coordinate system with the origin at point O. We need to resolve all forces into their x and y components. The forces are:

Force A: $ F_A = 8 \text{ kN} $ acting horizontally to the left. So, $ F_{Ax} = -8 \text{ kN} $, $ F_{Ay} = 0 $.
Force C: $ F_C = F = 12 \text{ kN} $ acting vertically upwards. So, $ F_{Cx} = 0 $, $ F_{Cy} = 12 \text{ kN} $.
Force D: $ F_D = 5 \text{ kN} $ acting at an angle of $ 45^\circ $ below the horizontal to the right. So, $ F_{Dx} = F_D \cos(45^\circ) = 5 \times \frac{\sqrt{2}}{2} = 3.5355 \text{ kN} $. And $ F_{Dy} = -F_D \sin(45^\circ) = -5 \times \frac{\sqrt{2}}{2} = -3.5355 \text{ kN} $.
Force B: Let the magnitude of force B be $ F_B $ and its angle with the negative x-axis be $ \theta $. It acts in the third quadrant. So, $ F_{Bx} = -F_B \cos(\theta) $. And $ F_{By} = -F_B \sin(\theta) $.

Step 2: Apply equilibrium equations

For equilibrium, the sum of forces in the x-direction and y-direction must be zero. $ \sum F_x = 0 $ $ F_{Ax} + F_{Bx} + F_{Cx} + F_{Dx} = 0 $ $ -8 - F_B \cos(\theta) + 0 + 3.5355 = 0 $ $ -F_B \cos(\theta) = 8 - 3.5355 $ $ -F_B \cos(\theta) = 4.4645 $ (Equation 1)

$ \sum F_y = 0 $ $ F_{Ay} + F_{By} + F_{Cy} + F_{Dy} = 0 $ $ 0 - F_B \sin(\theta) + 12 - 3.5355 = 0 $ $ -F_B \sin(\theta) = 3.5355 - 12 $ $ -F_B \sin(\theta) = -8.4645 $ $ F_B \sin(\theta) = 8.4645 $ (Equation 2)

Step 3: Solve for $ F_B $ and $ \theta $

From Equation 1, $ F_B \cos(\theta) = -4.4645 $. From Equation 2, $ F_B \sin(\theta) = 8.4645 $.

Divide Equation 2 by Equation 1: $ \frac{F_B \sin(\theta)}{F_B \cos(\theta)} = \frac{8.4645}{-4.4645} $ $ \tan(\theta) = -1.8959 $

Since $ \sin(\theta) $ is positive and $ \cos(\theta) $ is negative, $ \theta $ must be in the second quadrant. $ \theta = \arctan(-1.8959) + 180^\circ $ $ \theta \approx -62.9^\circ + 180^\circ $ $ \theta \approx 117.1^\circ $

Now substitute $ \theta $ back into Equation 2 to find $ F_B $: $ F_B \sin(117.1^\circ) = 8.4645 $ $ F_B (0.8899) = 8.4645 $ $ F_B = \frac{8.4645}{0.8899} $ $ F_B \approx 9.511 \text{ kN} $

The angle $ \theta $ in the problem statement is defined as the angle with the negative x-axis. Our calculated $ \theta $ is the angle with the positive x-axis. The angle $ \theta $ in the diagram is the angle between the negative x-axis and member B. So, the angle $ \theta_{diagram} = 180^\circ - \theta_{calculated} = 180^\circ - 117.1^\circ = 62.9^\circ $.

The force in member B is $ 9.51 \text{ kN} $ and its orientation $ \theta $ (as defined in the diagram) is $ 62.9^\circ $.