Questions: Acetylene gas C2H2 undergoes combustion to form carbon dioxide and water when it is used in the oxyacetylene torch for welding. Balance the reaction and answer the following questions. C2H2(g) + O2(g) -> CO2(g) + H2O(g) (a) How many grams of water can form if 113 g of acetylene is burned? (b) How many grams of acetylene react if 1.10 mol of CO2 are produced?
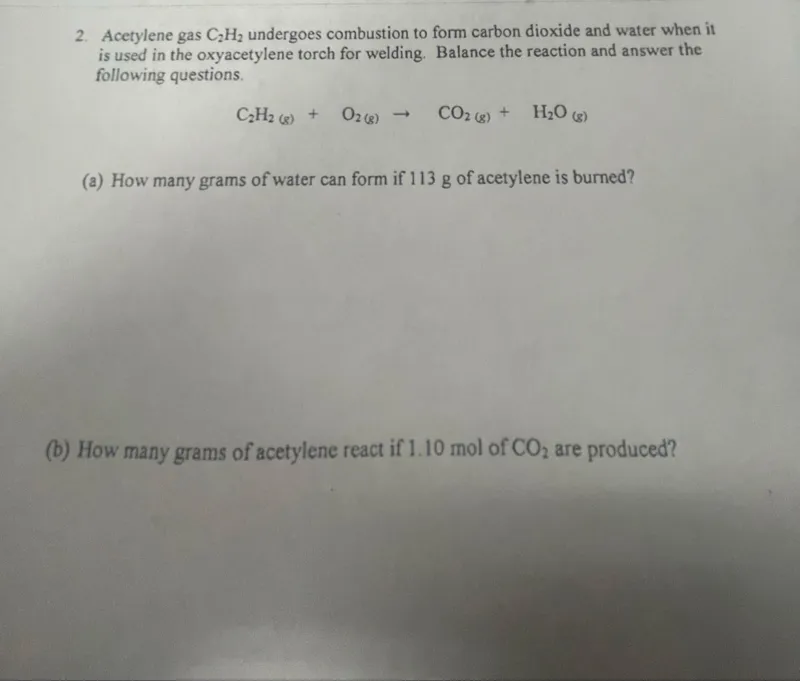
Transcript text: 2. Acetylene gas $\mathrm{C}_{2} \mathrm{H}_{2}$ undergoes combustion to form carbon dioxide and water when it is used in the oxyacetylene torch for welding. Balance the reaction and answer the following questions.
\[
\mathrm{C}_{2} \mathrm{H}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{CO}_{2(\mathrm{~g})}+\mathrm{H}_{2} \mathrm{O}_{(\mathrm{g})}
\]
(a) How many grams of water can form if 113 g of acetylene is burned?
(b) How many grams of acetylene react if 1.10 mol of $\mathrm{CO}_{2}$ are produced?





