Questions: Describe the solution to the system of equations graphed below. The system has infinitely many solutions of the form y=-x+3, where x is any real number. The system has no solutions. The system has a unique solution at (2,1). The system has a unique solution at (1,2).
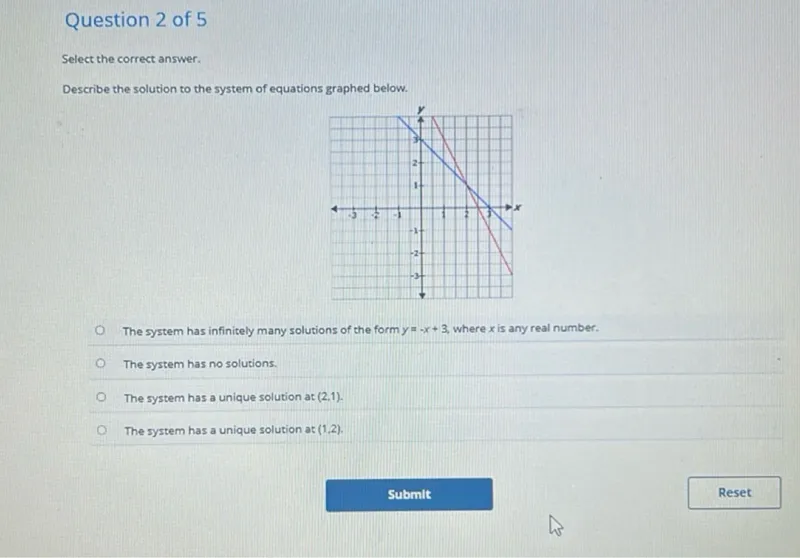
Transcript text: Describe the solution to the system of equations graphed below. The system has infinitely many solutions of the form $y=-x+3$, where $x$ is any real number. The system has no solutions. The system has a unique solution at (2,1). The system has a unique solution at (1,2).





