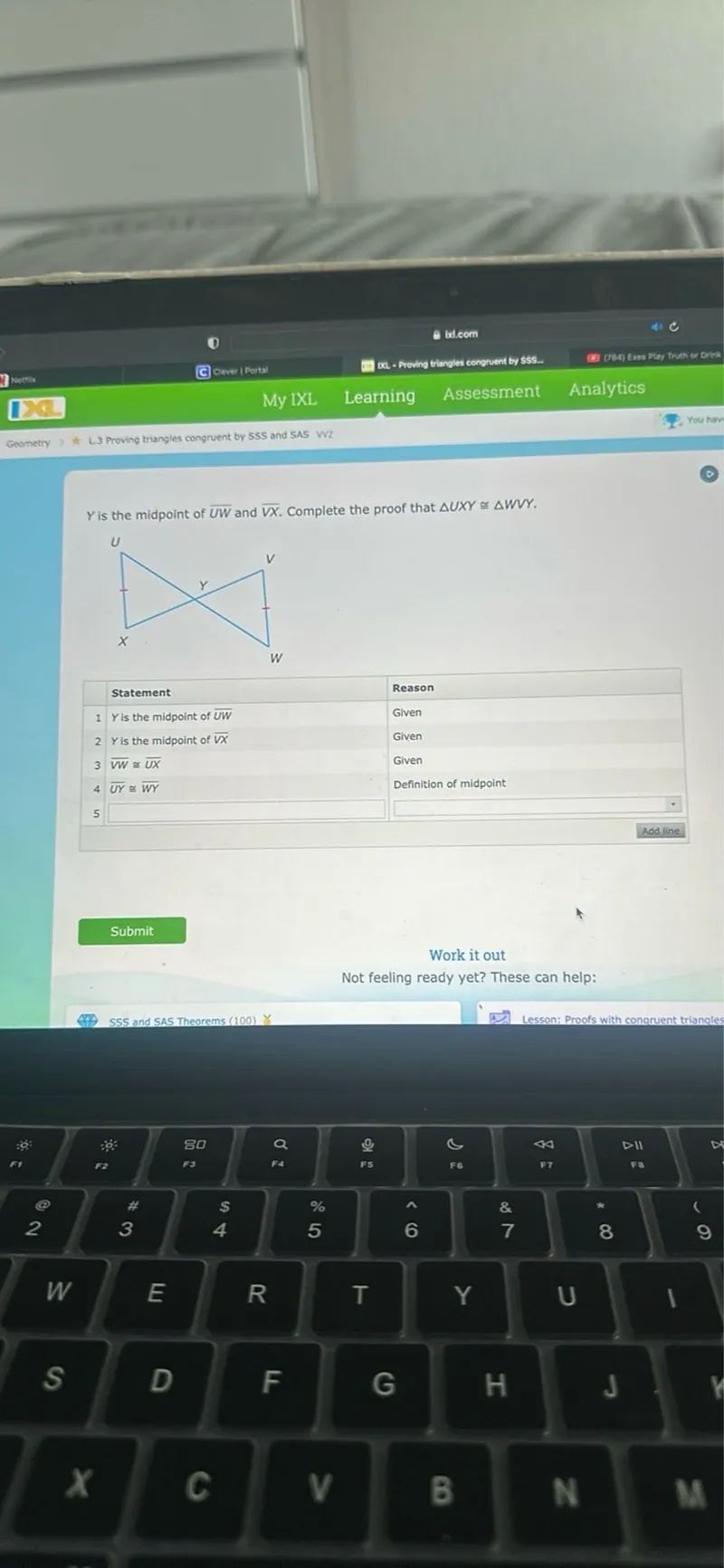
Questions: Geometry ≥+2.3 Proving triangles congruent by SSS and SAS WZ Y is the midpoint of UW and VX. Complete the proof that triangle UXY is congruent to triangle WVY. 1. Y is the midpoint of UW - Given 2. Y is the midpoint of VX - Given 3. VW is congruent to UX - Given 4. UY is congruent to WY - Definition of midpoint
Transcript text: Geometry $\geqslant+2.3$ Proving triangles congruent by SSS and SAS WZ
$Y$ is the midpoint of $\overline{U W}$ and $\overline{V X}$. Complete the proof that $\triangle U X Y \cong \triangle W V Y$.
\begin{tabular}{|l|l|l|}
\hline & Statement & Reason \\
\hline 1 & $Y$ is the midpoint of $\overline{U W}$ & Given \\
2 & $Y$ is the midpoint of $\overline{V X}$ & Given \\
3 & $\overline{V W} \cong \overline{U X}$ & Given \\
\hline 4 & $\overline{U Y} \cong \overline{W Y}$ & Definition of midpoint \\
5 & & \\
\hline & & \\
\hline
\end{tabular}





