Questions: Find the missing dimension of the regular hexagon shown to the right. Round to three significant digits if necessary. The missing dimension is approximately (1) in.

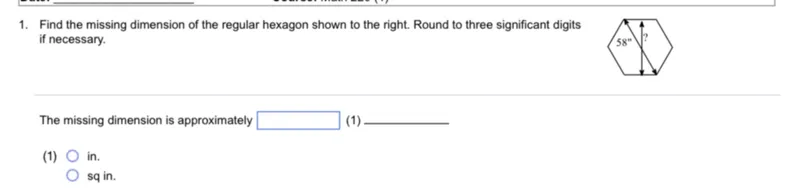
△ Find the missing dimension of the regular hexagon. ○ Analyze the hexagon ☼ The given figure is a regular hexagon. A regular hexagon has six equal sides and six equal angles. The interior angles of a regular hexagon are each 120°. The given diagonal of length 58" connects two non-adjacent vertices. This diagonal divides the hexagon into two congruent trapezoids. The missing dimension is the height of one of these trapezoids. ○ Relate the height to the side length ☼ Let $s$ be the side length of the hexagon. The diagonal of length 58" forms an isosceles triangle with two sides of length $s$. The base angles of this isosceles triangle are $\frac{180^\circ - 120^\circ}{2} = 30^\circ$. The height of the trapezoid can be found using trigonometry. The height of the trapezoid bisects the 120° angle, creating two 60° angles. We can consider the right triangle formed by the height, half of the diagonal, and the side of the hexagon. ○ Calculate the height ☼ Let $h$ be the height of the trapezoid. The height of the isosceles triangle with base 58" and base angles 30° is given by $h = \frac{1}{2} \cdot 58 \cdot \tan{60^\circ}$ $h = 29 \sqrt{3}$ $h \approx 50.23$ The height is approximately 50.2 inches.

✧ $\boxed{50.2 \text{ in.}}$

☺ 50.2 in.