Questions: Rationalize the denominator. 5 / (3 + √11) 5 / (3 + √11) = (Simplify your answer. Type an exact answer, using radicals)
Transcript text: 121. Module 1 MLM HW - Algeb
Do Homew
mylab.pearson.com/Student/PlayerHomework. aspx?homeworkld=69003
121 - College Algebra [OL]
121. Module 1 MLM HW - Algebra
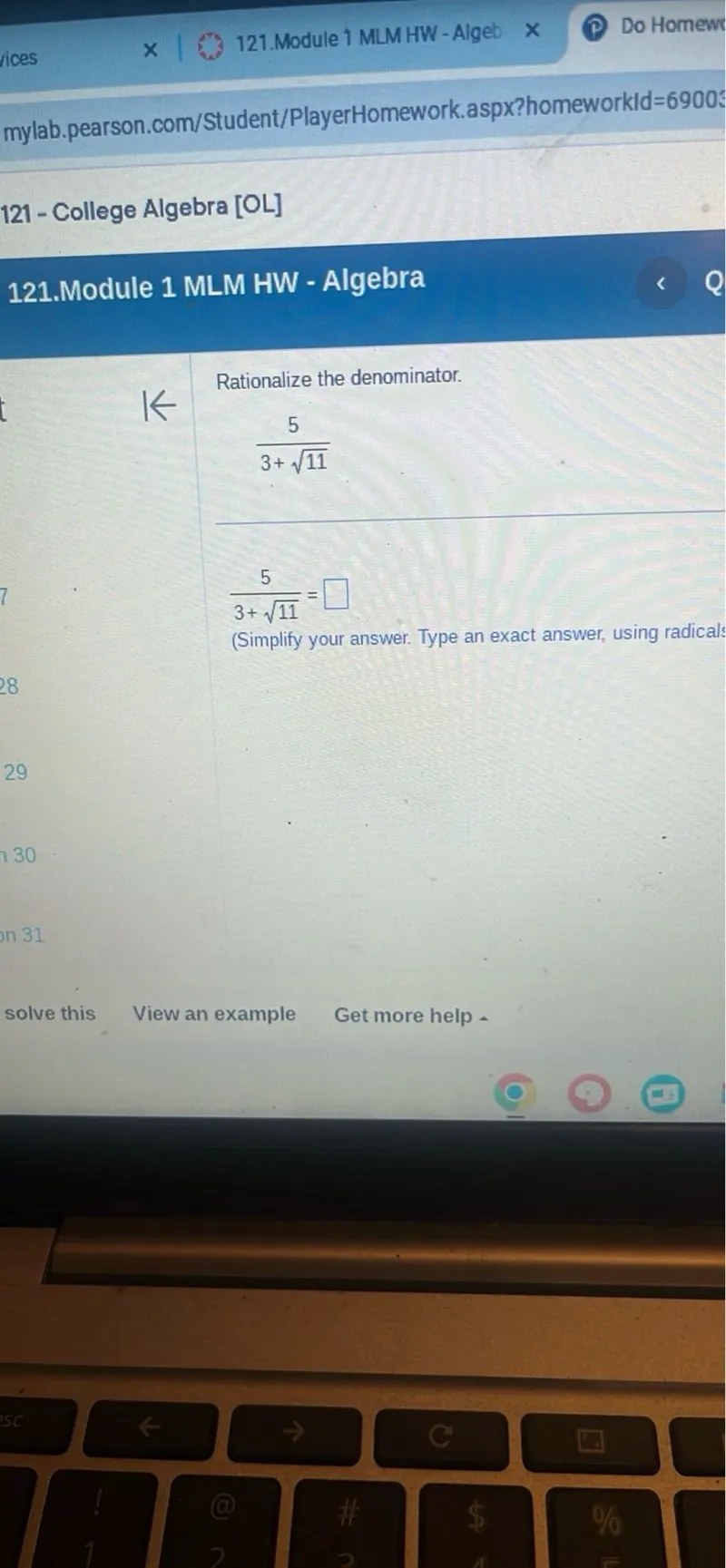
Rationalize the denominator.
\[
\frac{5}{3+\sqrt{11}}
\]
\[
\frac{5}{3+\sqrt{11}}=
\]
$\square$
(Simplify your answer. Type an exact answer, using radicals
solve this
View an example
Get more help .





