Questions: Which function describes the graph? f(x)=2x^3+3 f(x)=3x^2+2 f(x)=-2x^2+3 f(x)=-3x^3+2

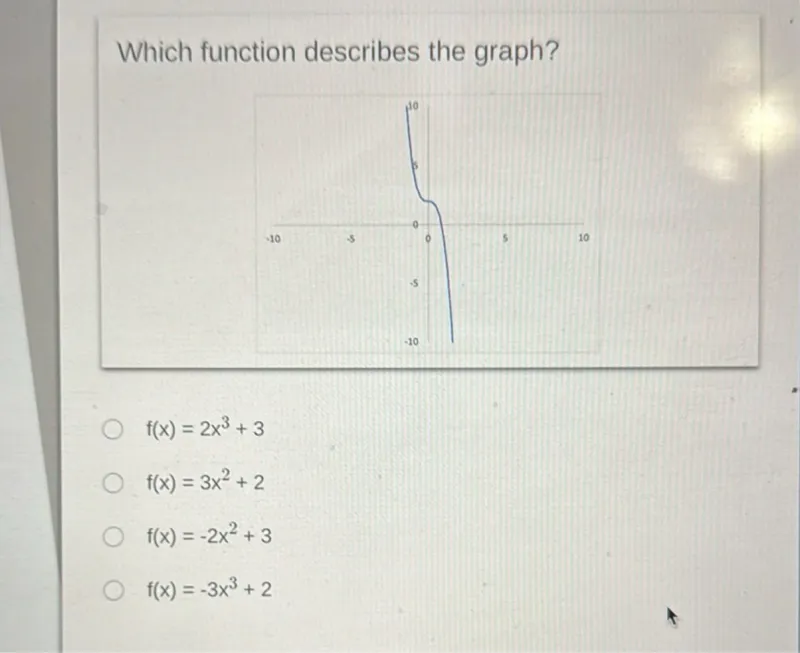
Which function describes the graph? f(x)=2x^3+3 f(x)=3x^2+2 f(x)=-2x^2+3 f(x)=-3x^3+2
Transcript text: Which function describes the graph? $f(x)=2 x^{3}+3$ $f(x)=3 x^{2}+2$ $f(x)=-2 x^{2}+3$ $f(x)=-3 x^{3}+2$
failed

Solution

failed
failed

Solution Steps

Step 1: Analyze the graph's behavior

The graph passes through the point (0, 2). It also has a general shape that decreases as x increases, suggesting a negative leading coefficient and an even or odd degree.

Step 2: Evaluate options at x=0

Let's evaluate each function at $x=0$ to see which one passes through the point $(0, 2)$.

  1. $f(0) = 2(0)^3 + 3 = 3$
  2. $f(0) = 3(0)^2 + 2 = 2$
  3. $f(0) = -2(0)^2 + 3 = 3$
  4. $f(0) = -3(0)^3 + 2 = 2$

Options 2 and 4 pass through (0,2).

Step 3: Analyze the shape of the graph

The graph appears to have an inflection point around $x=0$. This behavior is typical of a cubic function, not a quadratic. Option 2 is quadratic, while option 4 is cubic.

Final Answer

\\(\boxed{f(x)=-3 x^{3}+2}\\)

Was this solution helpful?
failed
Unhelpful
failed
Helpful

Questions asked by other users

failedAnswered
Question 6 1 pt When homologous chromosomes cross over, what is the result? Two sister chromatids exchange identical pieces of DNA. Two sister chromatids get tangled, resulting in one altering the sequence of its DNA. Each of the four DNA strands of a homologous pair is broken, and the pieces are mixed. Specific proteins break the two strands of nonsister chromatids and re-join them. Question 7 1 pts
failedAnswered
Arturo is a documented migrant worker in the United States. He was injured while working and went to the hospital for treatment. While he was at the hospital, the doctors and nurses had difficulty communicating with Arturo because he speaks some English but not enough to understand medical terminology. The hospital does not have a translator on staff. This is an example of: institutional racism prejudice scapegoating discrimination
failedAnswered
Elemental sulfur exists in two crystalline forms, rhombic and monoclinic. From the following data, calculate the equilibrium temperature at which monoclinic sulfur and rhombic sulfur are in equilibrium. - Delta Hf°(kJ / mol) and S°(J / K mol): S (rhombic): 0, 31.880 S (monoclinic): 0.30, 32.546 450 K 200 K -200 K -450 K 0 K
failedAnswered
1. The price elasticity of demand measures a. buyers' responsiveness to a change in the price of a good. b. the extent to which demand increases as additional buyers enter the market. c. how much more of a good consumers will demand when incomes rise. d. the movement along a supply curve when there is a change in demand.
failedAnswered
Solve the absolute value equation. 3a+4=4a-2 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The solution set is . (Type an integer or a simplified fraction. Use a comma to separate answers as needed.) B. The solution set is ∅.