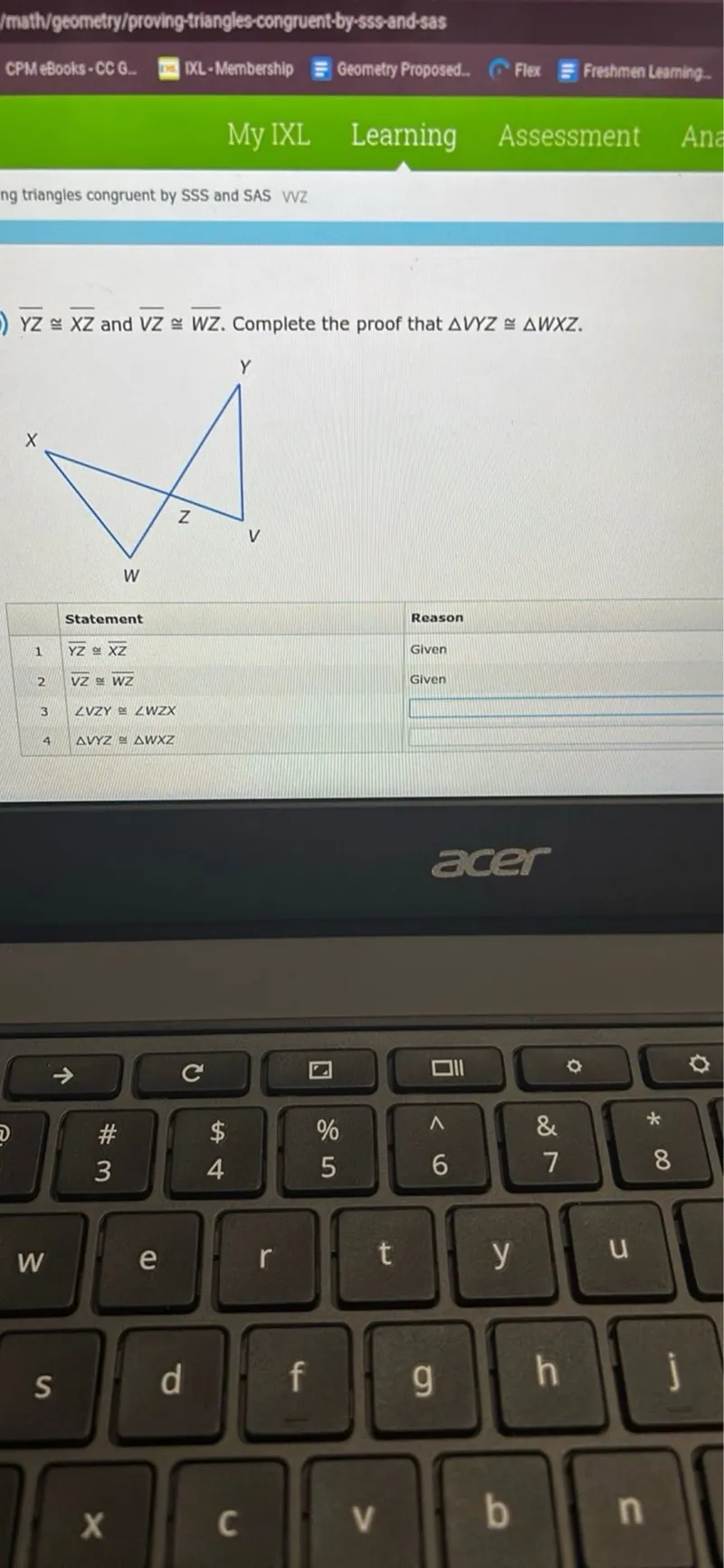
Questions: Proving triangles congruent by SSS and SAS Y Z ≅ X Z and V Z ≅ W Z. Complete the proof that triangle V Y Z ≅ triangle W X Z.

Solution Steps

We are given that $\overline{YZ} \cong \overline{XZ}$ and $\overline{VZ} \cong \overline{WZ}$.

Observe that $\angle YZV$ and $\angle XZW$ are vertical angles.

Since vertical angles are congruent, we have $\angle YZV \cong \angle XZW$.

We have two pairs of congruent sides and a pair of congruent angles between them: \begin{itemize} \item $\overline{YZ} \cong \overline{XZ}$ \item $\overline{VZ} \cong \overline{WZ}$ \item $\angle YZV \cong \angle XZW$ \end{itemize} Therefore, by the Side-Angle-Side (SAS) Congruence Postulate, we can conclude that $\triangle VYZ \cong \triangle WXZ$.

Final Answer