Questions: Find all solutions to 2 cos(θ) = -√2 on the interval 0 ≤ θ < 2π θ=

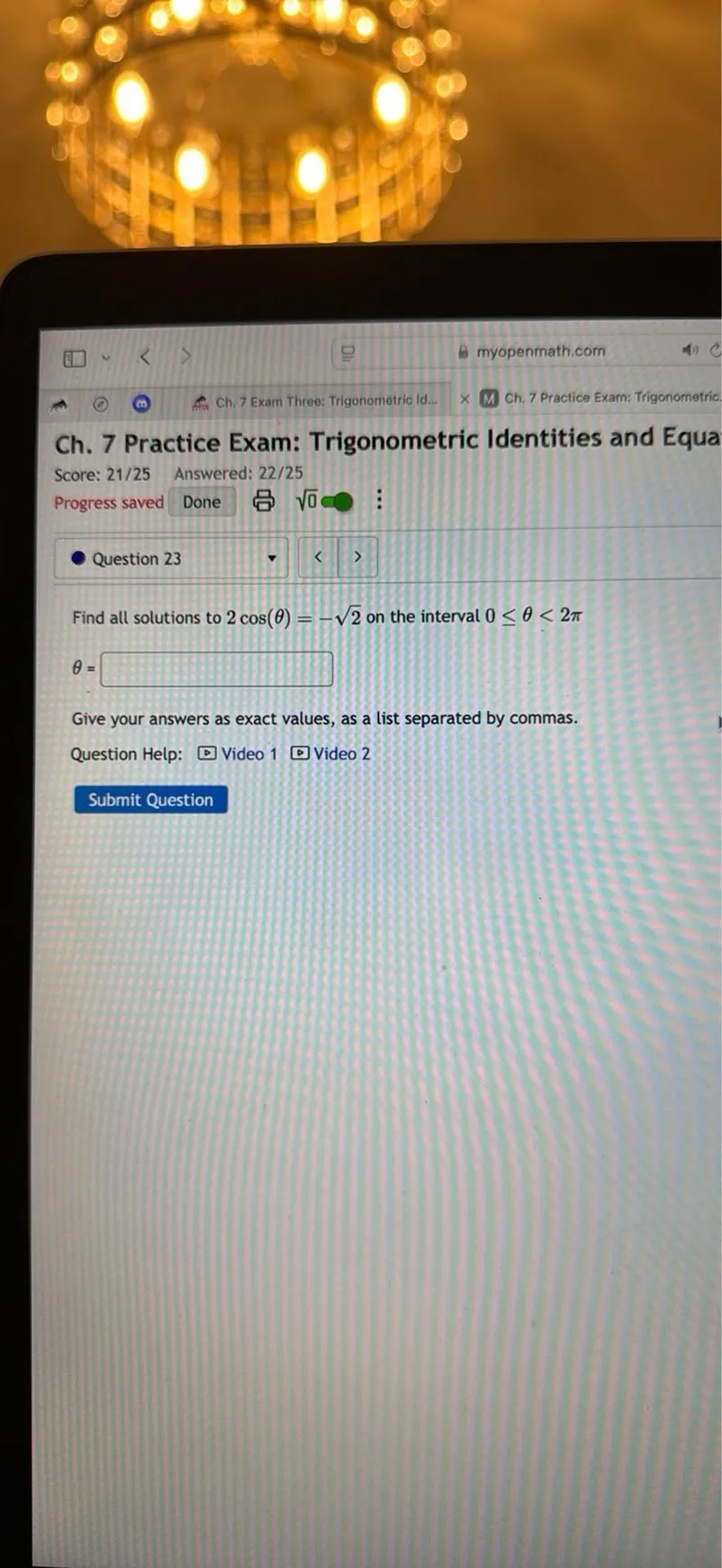
Transcript text: Find all solutions to $2 \cos (\theta)=-\sqrt{2}$ on the interval $0 \leq \theta<2 \pi$ \[ \theta= \]

Solution

Solution Steps

Step 1: Isolate $\cos(\theta)$

Starting with the equation $2 \cos(\theta) = -\sqrt{2}$, we divide both sides by 2 to isolate $\cos(\theta)$: \[ \cos(\theta) = -\frac{\sqrt{2}}{2} \]

Step 2: Identify the Angles

Next, we determine the angles $\theta$ for which $\cos(\theta) = -\frac{\sqrt{2}}{2}$. The cosine function is negative in the second and third quadrants. The reference angle where $\cos(\theta) = \frac{\sqrt{2}}{2}$ is $\frac{\pi}{4}$. Therefore, the angles in the specified quadrants are: \[ \theta = \pi - \frac{\pi}{4} = \frac{3\pi}{4} \quad \text{(second quadrant)} \] \[ \theta = \pi + \frac{\pi}{4} = \frac{5\pi}{4} \quad \text{(third quadrant)} \]

Step 3: List the Solutions

The solutions to the equation $2 \cos(\theta) = -\sqrt{2}$ in the interval $0 \leq \theta < 2\pi$ are: \[ \theta = \frac{3\pi}{4}, \frac{5\pi}{4} \]