Questions: The angle bisectors of triangle ABC are AV, BV, and CV. They meet at a single point V. (In other words, V is the incenter of triangle ABC) Suppose SV=8,8V=21, m angle S8T=32 degrees, and m angle UCV=26 degrees, Find the following measures.
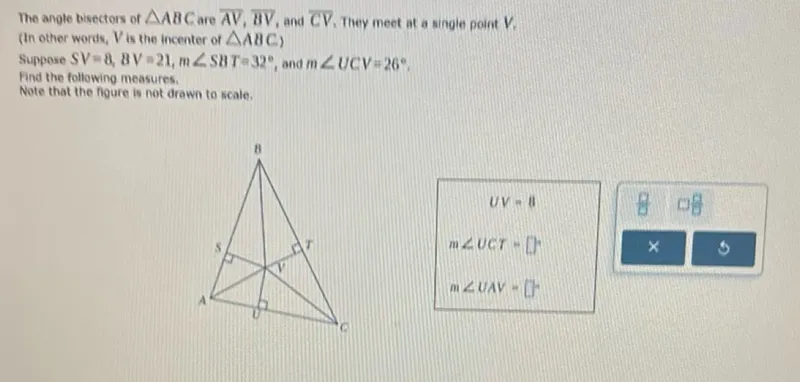
Transcript text: The angle bisectors of $\triangle A B C$ are $\overline{A V}, \overline{B V}$, and $\overline{C V}$. They meet at a single point $V$.
(In other words, $V$ is the incenter of $\triangle A B C$ )
Suppose $S V=8,8 V=21, m \angle S 8 T=32^{\circ}$, and $m \angle U C V=26^{\circ}$,
Find the following measures.





