Questions: Find the intervals on which f(x) is increasing, the intervals on which f(x) is decreasing, and the local extrema, f(x)=x^3+5x-14 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is increasing on . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never increasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is decreasing on . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never decreasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type integers or simplified fractions. Use a comma to separate answers as needed.) A. The function has local maxima f(c)= and local minima f(c)= . B. The function has local minima f(c)= , and no local maxima.

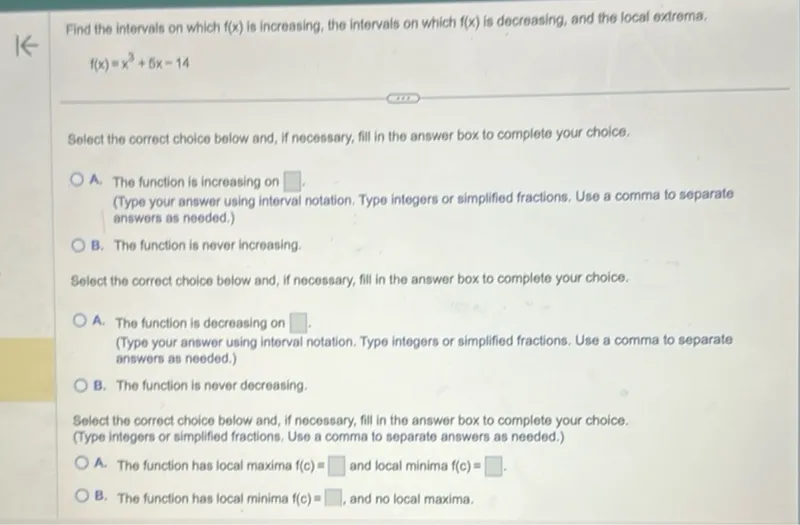
Transcript text: Find the intervals on which $f(x)$ is increasing, the intervals on which $f(x)$ is decreasing, and the local extrema, \[ f(x)=x^{3}+5 x-14 \] Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is increasing on $\square$ . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never increasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The function is decreasing on $\square$ . (Type your answer using interval notation. Type integers or simplified fractions. Use a comma to separate answers as needed.) B. The function is never decreasing. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (Type integers or simplified fractions. Use a comma to separate answers as needed.) A. The function has local maxima $f(c)=$ $\square$ and local minima $f(c)=$ $\square$ . B. The function has local minima $f(c)=$ $\square$ , and no local maxima.