Questions: Write an equation for a linear function given a graph of (f(x)) shown below. (f(x)=square)
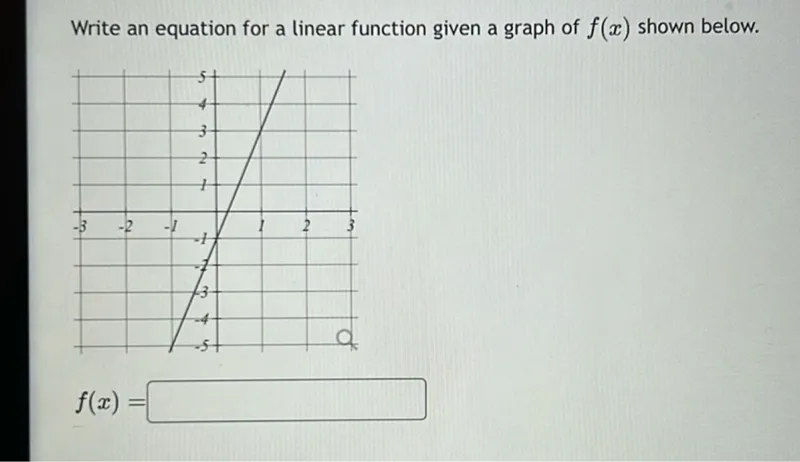
Transcript text: Write an equation for a linear function given a graph of $f(x)$ shown below.
\[
f(x)=\square
\]





