Questions: Four distributions, labeled (a), (b), (c), and (d) are represented below by their histograms. Each distribution is made of 9 measurements. Without performing any calculations, order their respective means μa, μb, μc, and μd. Enter the four subscripts appropriately below.

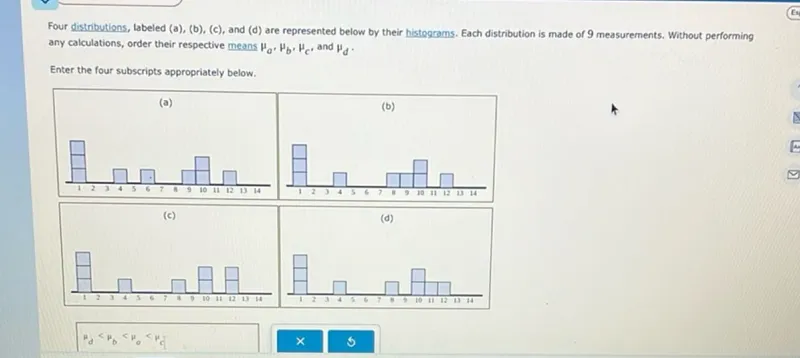
Four distributions, labeled (a), (b), (c), and (d) are represented below by their histograms. Each distribution is made of 9 measurements. Without performing any calculations, order their respective means μa, μb, μc, and μd. Enter the four subscripts appropriately below.

Transcript text: Four distributions, labeled (a), (b), (c), and (d) are represented below by their histograms. Each distribution is made of 9 measurements. Without performing any calculations, order their respective means $\mu_{a}, \mu_{b}, \mu_{c}$, and $\mu_{d}$. Enter the four subscripts appropriately below.

Solution

△ Order the means of the distributions represented by the histograms. ○ Assess the balancing point of each histogram visually. ☼ The mean represents the "center of mass" or balancing point of the histogram. Observing the distributions:

(a): Data is concentrated on the left side, with some values to the right. The balance point appears around 4-5.
(b): Data leans slightly towards the right, with more symmetry and the bulk around 9-10.
(c): Data is mostly on the left, with a few values in the middle and right. Most of the weight is at the low end, making the mean lower compared to others.
(d): Data leans towards the right, with most values clumped around 10-12. ○ Compare the means visually. ☼ Comparing the balancing points: (c) has the lowest mean, followed by (a). (b) has a smaller mean than (d). Thus, the order is $ \mu_c < \mu_a < \mu_b < \mu_d $. ✧ The ordered means are $ \mu_c < \mu_a < \mu_b < \mu_d $. ☺ μ_c < μ_a < μ_b < μ_d

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

Next >

Thank you for your feedback.

Copied!