Questions: Use the given information to find n(A × B) and n(B × A). n(A)=44 and n(B)=7 Find the number of elements in the set A × B. n(A × B)=308 (Type an integer.) Find the number of elements in the set B × A. n(B × A)= (Type an integer.)

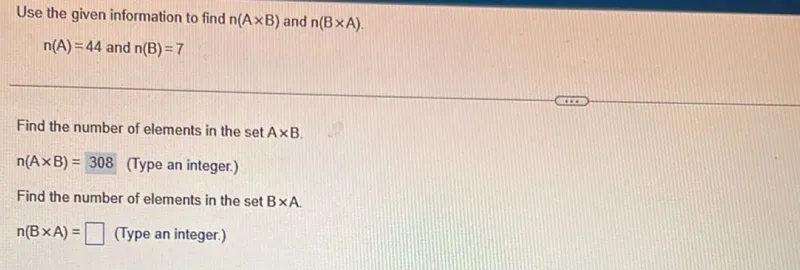
Use the given information to find n(A × B) and n(B × A).

n(A)=44 and n(B)=7

Find the number of elements in the set A × B.

n(A × B)=308 (Type an integer.)

Find the number of elements in the set B × A.

n(B × A)= (Type an integer.)

Transcript text: Use the given information to find $n(A \times B)$ and $n(B \times A)$. \[ n(A)=44 \text { and } n(B)=7 \] Find the number of elements in the $\operatorname{set} A \times B$. \[ n(A \times B)=308 \text { (Type an integer.) } \] Find the number of elements in the $\operatorname{set} B \times A$. \[ n(B \times A)=\square \text { (Type an integer.) } \]

Solution

Solution Steps

Step 1: Understand the problem

We are given the number of elements in sets $ A $ and $ B $, which are $ n(A) = 44 $ and $ n(B) = 7 $, respectively. We need to find the number of elements in the Cartesian products $ A \times B $ and $ B \times A $.

Step 2: Recall the formula for the Cartesian product

The number of elements in the Cartesian product $ A \times B $ is given by: \[ n(A \times B) = n(A) \times n(B) \] Similarly, the number of elements in $ B \times A $ is: \[ n(B \times A) = n(B) \times n(A) \]

Step 3: Calculate $ n(A \times B) $

Using the formula: \[ n(A \times B) = n(A) \times n(B) = 44 \times 7 = 308 \]

Step 4: Calculate $ n(B \times A) $

Using the formula: \[ n(B \times A) = n(B) \times n(A) = 7 \times 44 = 308 \]

Step 5: Verify the result

Since $ n(A \times B) = n(B \times A) $, the number of elements in both Cartesian products is the same, which is 308.