Questions: Simplify answers and show your work. 2) (4 points) Write an equation for the function graphed.

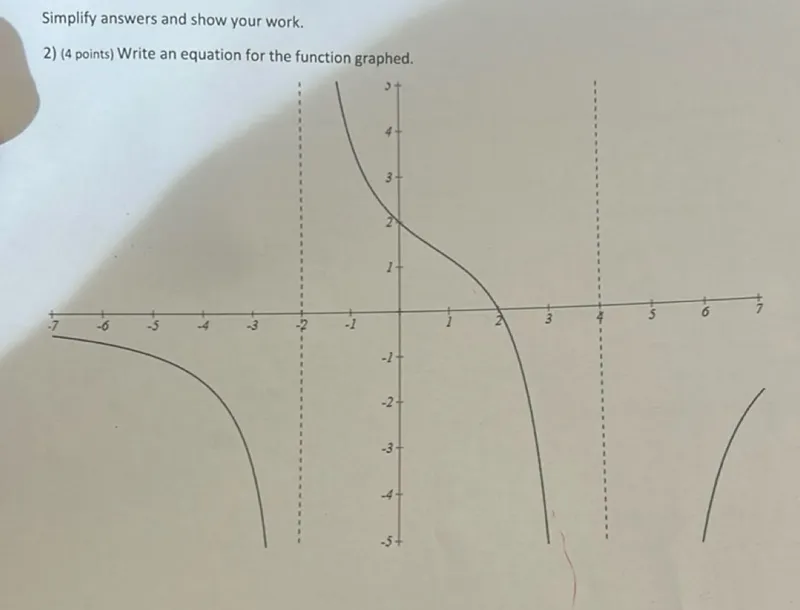
Write an equation for the function graphed.

Find the vertical asymptotes.

The vertical asymptotes are at \(x = -2\) and \(x = 4\).

Find the horizontal asymptote.

The horizontal asymptote is at \(y = 0\).

Determine the general form of the equation.

Since there are two vertical asymptotes and a horizontal asymptote at \(y=0\), the general form of the equation is \[y = \frac{a}{(x - h)(x - k)}\] where \(h\) and \(k\) are the vertical asymptotes and \(a\) is a constant.

Substitute the vertical asymptotes into the general form.

\[y = \frac{a}{(x - (-2))(x - 4)} = \frac{a}{(x + 2)(x - 4)}\]

Find the value of \(a\).

The graph passes through the point \((0, 2)\). Substitute this point into the equation: \[2 = \frac{a}{(0 + 2)(0 - 4)}\] \[2 = \frac{a}{-8}\] \[a = -16\]

Write the final equation.

The equation is \[y = \frac{-16}{(x + 2)(x - 4)}\]

\(\boxed{y = \frac{-16}{(x+2)(x-4)}}\)

\(y = \frac{-16}{(x+2)(x-4)}\)