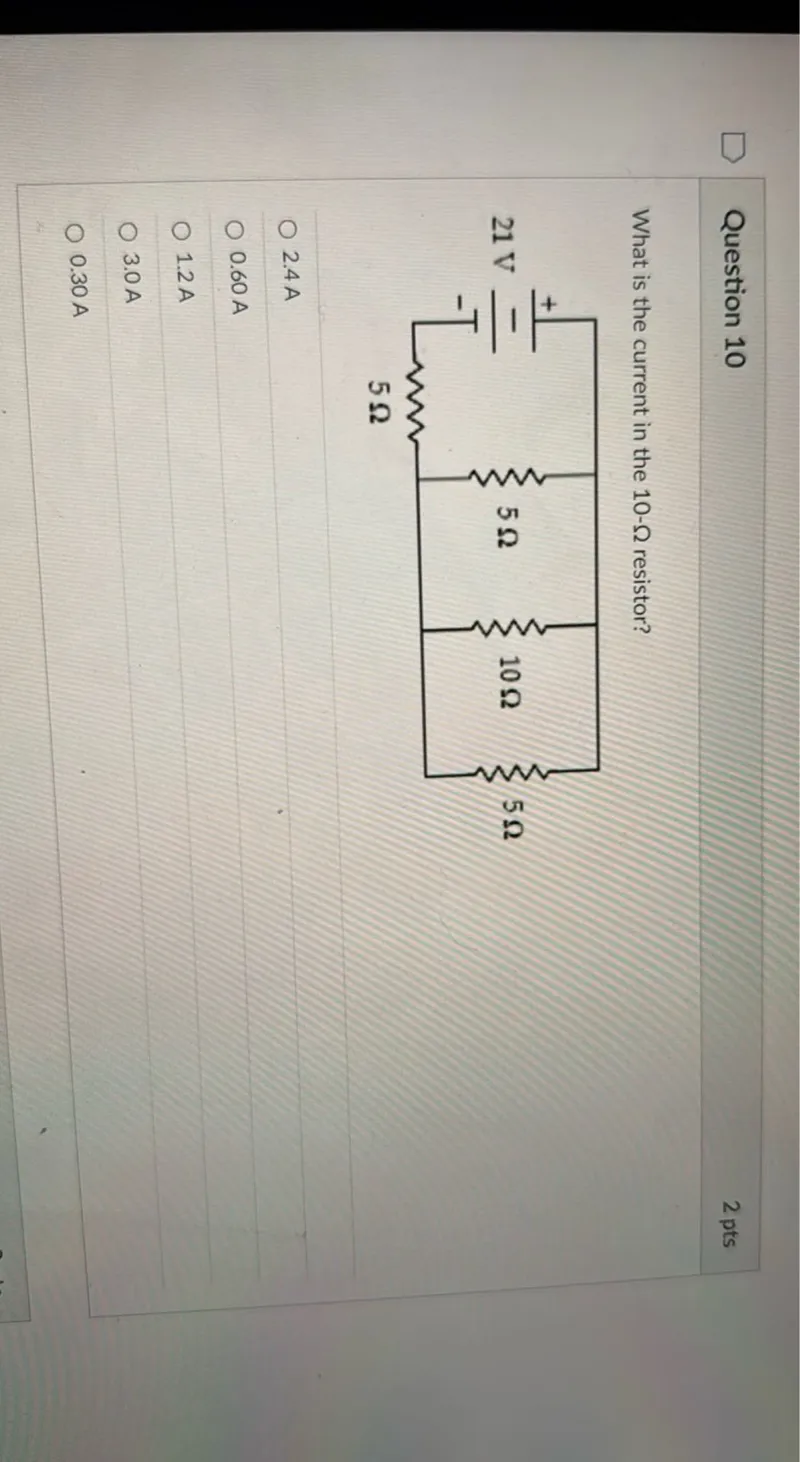
Calculate the current in the $10-\Omega$ resistor.
Identify the circuit configuration.
The circuit consists of a 21 V voltage source, a $5-\Omega$ resistor in series with the source, and three resistors ($5-\Omega$, $10-\Omega$, and $5-\Omega$) connected in parallel across the series resistor and the voltage source.
Calculate the equivalent resistance of the parallel combination.
The equivalent resistance \(R_p\) of the three parallel resistors is given by:
\( \frac{1}{R_p} = \frac{1}{5 \Omega} + \frac{1}{10 \Omega} + \frac{1}{5 \Omega} \)
\( \frac{1}{R_p} = \frac{2}{10 \Omega} + \frac{1}{10 \Omega} + \frac{2}{10 \Omega} = \frac{5}{10 \Omega} \)
\( R_p = \frac{10 \Omega}{5} = 2 \Omega \)
Calculate the total equivalent resistance of the circuit.
The total equivalent resistance \(R_{total}\) is the sum of the series resistor and the equivalent parallel resistance:
\( R_{total} = 5 \Omega + R_p = 5 \Omega + 2 \Omega = 7 \Omega \)
Calculate the total current flowing from the voltage source.
Using Ohm's Law, the total current \(I_{total}\) is:
\( I_{total} = \frac{V}{R_{total}} = \frac{21 V}{7 \Omega} = 3 A \)
Calculate the voltage across the parallel combination of resistors.
The voltage across the parallel combination \(V_p\) is the voltage across the equivalent parallel resistance, which can be found by subtracting the voltage drop across the series resistor from the total voltage:
\( V_p = V - I_{total} \times 5 \Omega = 21 V - 3 A \times 5 \Omega = 21 V - 15 V = 6 V \)
Alternatively, the voltage across the parallel combination is also given by:
\( V_p = I_{total} \times R_p = 3 A \times 2 \Omega = 6 V \)
Calculate the current in the $10-\Omega$ resistor.
Using Ohm's Law, the current \(I_{10\Omega}\) in the $10-\Omega$ resistor is:
\( I_{10\Omega} = \frac{V_p}{10 \Omega} = \frac{6 V}{10 \Omega} = 0.6 A \)
The current in the $10-\Omega$ resistor is \( \boxed{0.60 A} \).
The current in the $10-\Omega$ resistor is \( \boxed{0.60 A} \).