Questions: In the circuit shown in the figure, an ideal ohmmeter is connected across ab with the switch S open. All the connecting leads have negligible resistance. The reading of the ohmmeter will be closest to
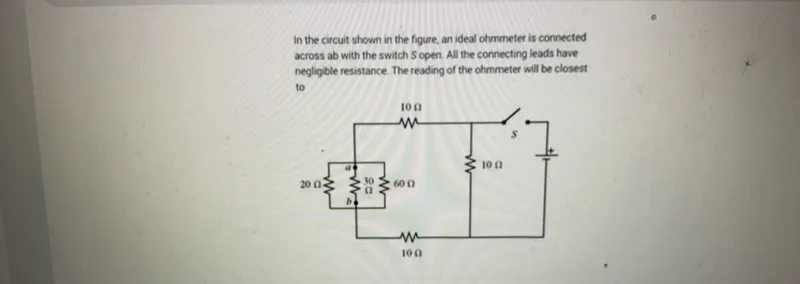
Transcript text: In the circuit shown in the figure, an ideal ohmmeter is connected across ab with the switch $S$ open. All the connecting leads have negligible resistance. The reading of the ohmmeter will be closest to





