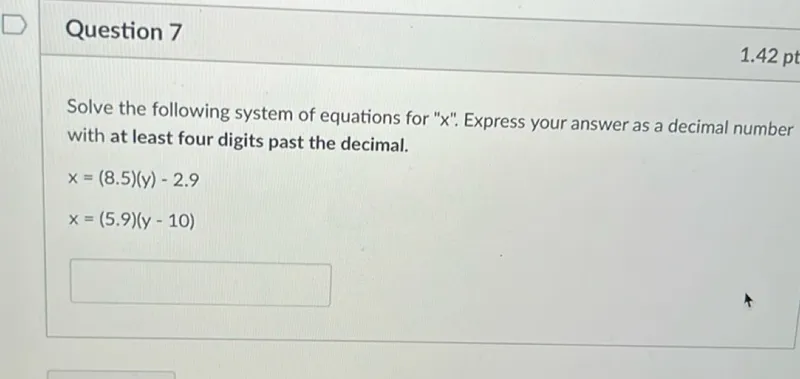
Questions: Solve the following system of equations for "x". Express your answer as a decimal number with at least four digits past the decimal. x=(8.5)(y)-2.9 x=(5.9)(y-10)

Solve the system of equations for \( x \).

Express both equations in terms of \( y \).

The first equation is \( x = 8.5y - 2.9 \) and the second equation is \( x = 5.9(y - 10) \). We can rewrite the second equation as \( x = 5.9y - 59.0 \).

Set the two expressions for \( x \) equal to each other.

Setting \( 8.5y - 2.9 = 5.9y - 59.0 \) allows us to solve for \( y \).

Solve for \( y \).

Rearranging gives \( 8.5y - 5.9y = -59.0 + 2.9 \), which simplifies to \( 2.6y = -56.1 \). Thus, \( y = \frac{-56.1}{2.6} = -21.5769230769231 \).

Substitute \( y \) back into one of the original equations to find \( x \).

Using \( x = 8.5(-21.5769230769231) - 2.9 \), we find \( x = -186.303846153846 \).

The value of \( x \) is \( \boxed{-186.3038} \).

The final answer is \( x = -186.3038 \).