Questions: Factor the perfect square trinomial. x^2+4 x+4 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. x^2+4 x+4= (Factor completely.) B. The polynomial is prime.
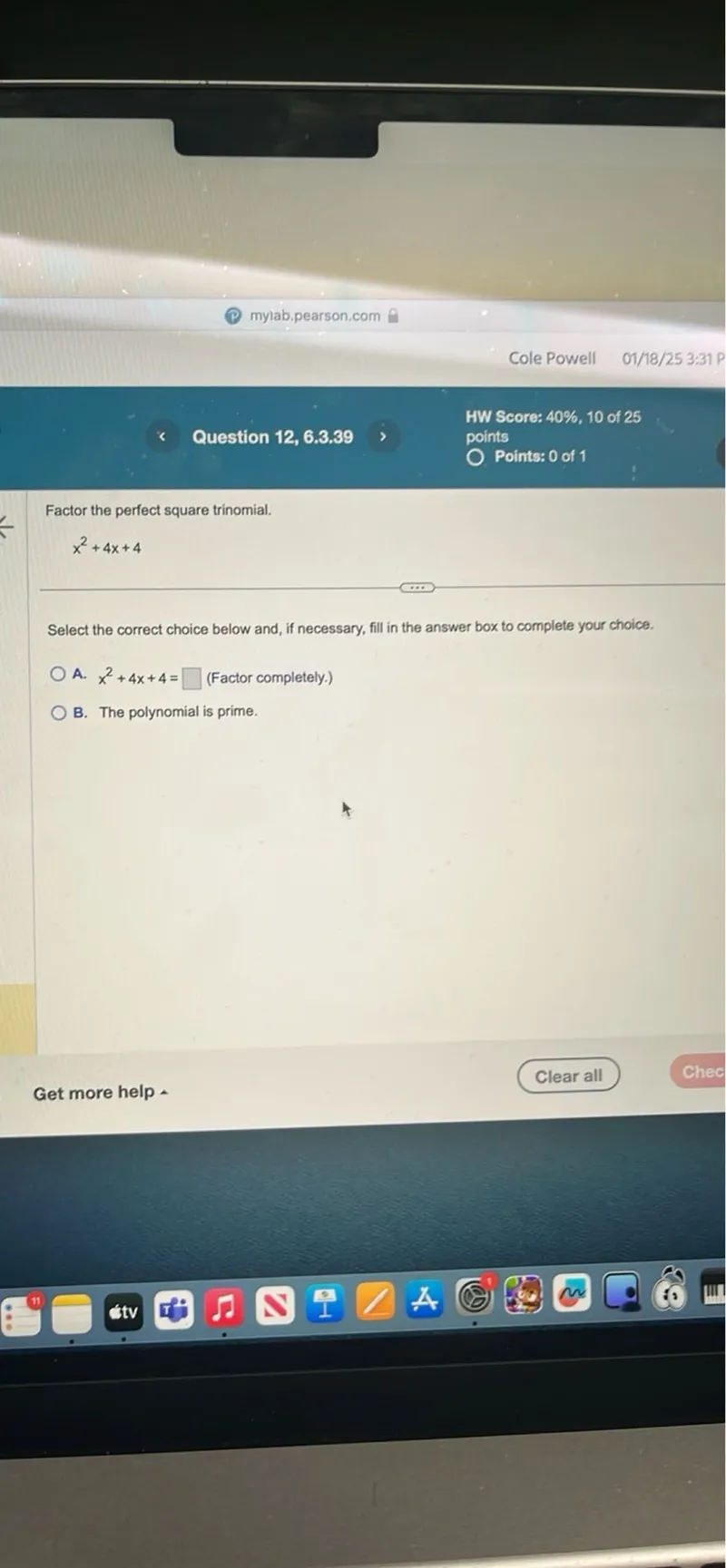
Transcript text: Factor the perfect square trinomial.
\[
x^{2}+4 x+4
\]
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. $x^{2}+4 x+4=$ $\square$ (Factor completely.)
B. The polynomial is prime.





