Questions: 15. Given that z is a standard normal random variable, find z for each situation. a. The area to the left of z is .2119. b. The area between -z and z is .9030. c. The area between -z and z is .2052. d. The area to the left of z is .9948. e. The area to the right of z is .6915.
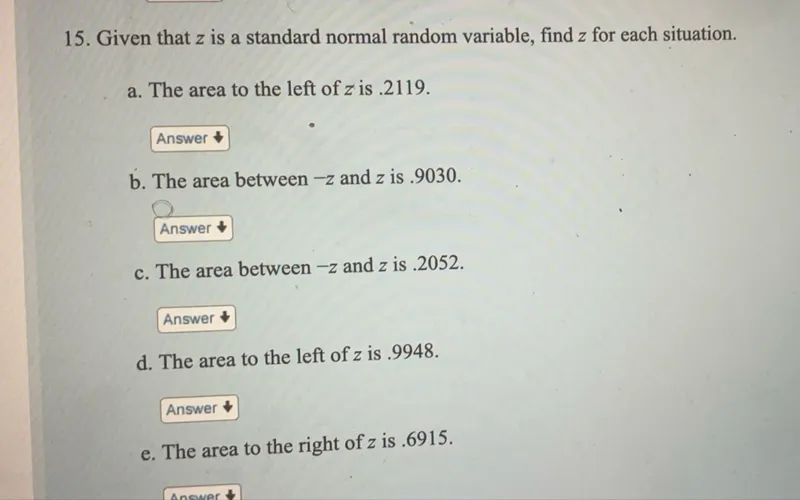
Transcript text: 15. Given that $z$ is a standard normal random variable, find $z$ for each situation.
a. The area to the left of $z$ is .2119.
b. The area between $-z$ and $z$ is .9030.
c. The area between $-z$ and $z$ is .2052.
d. The area to the left of $z$ is .9948.
e. The area to the right of $z$ is .6915.





