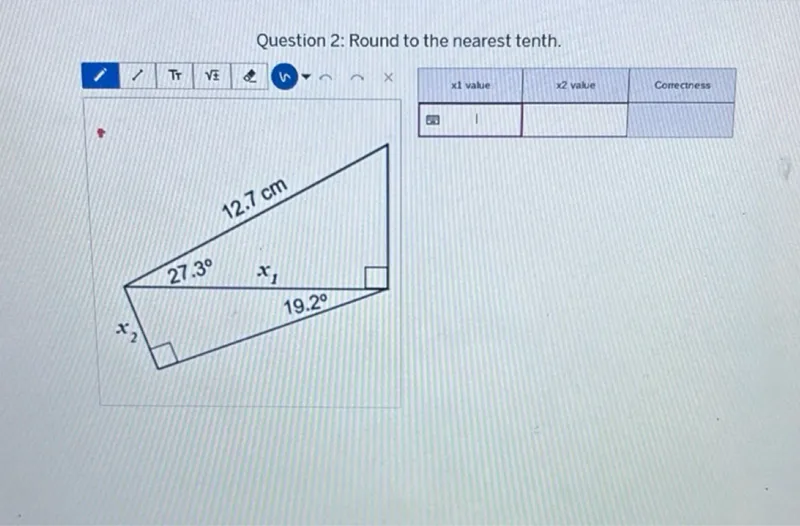
Find \(x_1\) and \(x_2\).
Find \(h\) using the upper triangle.
In the upper triangle, we have an angle of 27.3° and the hypotenuse is 12.7 cm. We can use the sine function to find the height \(h\):
\(\sin(27.3^\circ) = \frac{h}{12.7}\)
\(h = 12.7 \times \sin(27.3^\circ)\)
\(h \approx 12.7 \times 0.4592\)
\(h \approx 5.83 \text{ cm}\)
Find \(x_1\) using the lower triangle.
In the lower triangle, we have an angle of 19.2° and the height \(h \approx 5.83\). We can use the tangent function to find \(x_1\):
\(\tan(19.2^\circ) = \frac{h}{x_1}\)
\(x_1 = \frac{h}{\tan(19.2^\circ)}\)
\(x_1 \approx \frac{5.83}{0.3487}\)
\(x_1 \approx 16.72 \text{ cm}\)
Find \(x_2\) using the lower triangle.
In the lower triangle, we have an angle of 19.2° and \(x_1 \approx 16.72\). We can use the cosine function to find \(x_2\):
\(\cos(19.2^\circ) = \frac{x_1}{x_2}\)
\(x_2 = \frac{x_1}{\cos(19.2^\circ)}\)
\(x_2 \approx \frac{16.72}{0.9446}\)
\(x_2 \approx 17.70 \text{ cm}\)
\(x_1 \approx \boxed{16.7}\) cm, \(x_2 \approx \boxed{17.7}\) cm
\(x_1 \approx \boxed{16.7}\) cm
\(x_2 \approx \boxed{17.7}\) cm