Questions: The function g is defined by the following rule. g(x) = (1/6)^x Find g(x) for each x-value in the table. x g(x) -2 -1 0 1

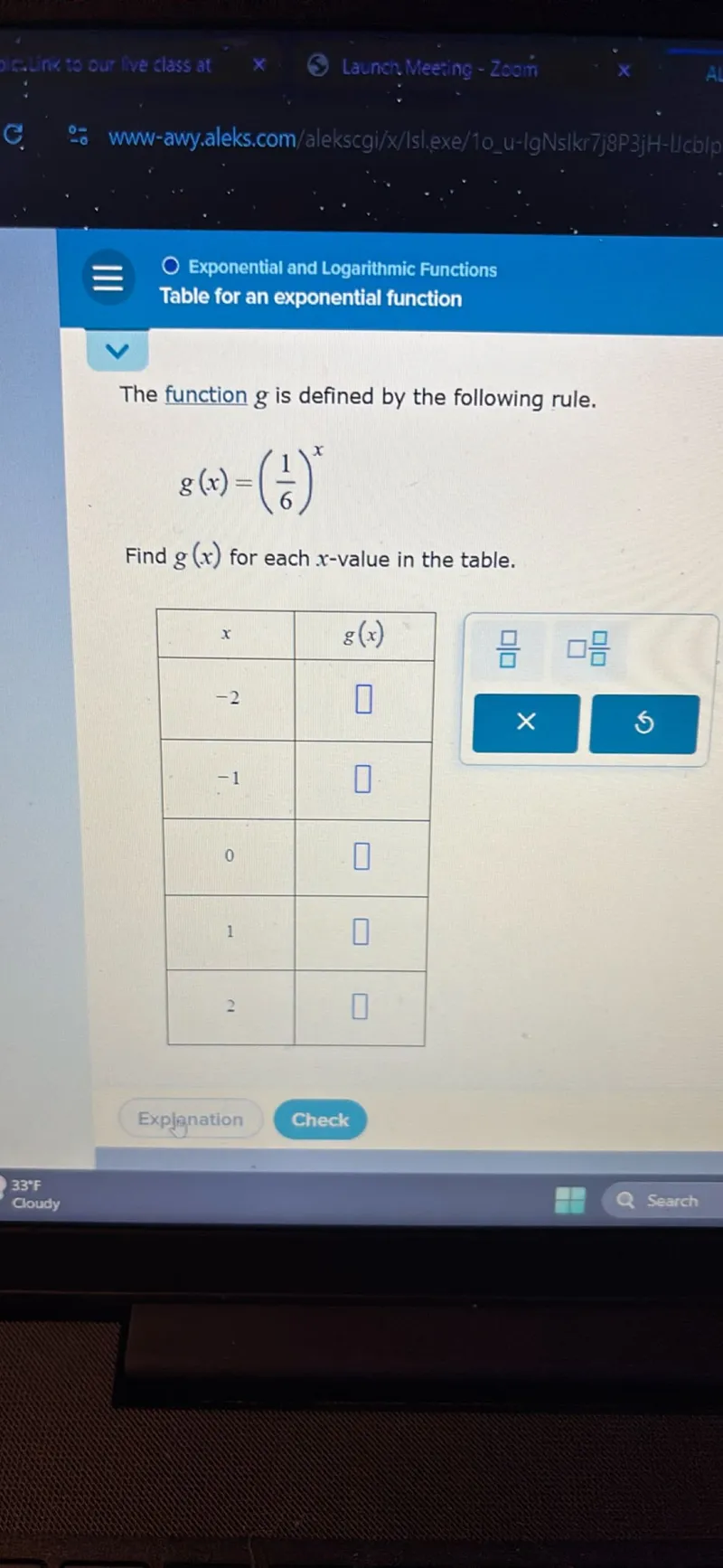
Transcript text: The function $g$ is defined by the following rule. \[ g(x)=\left(\frac{1}{6}\right)^{x} \] Find $g(x)$ for each $x$-value in the table. \begin{tabular}{|c|c|} \hline$x$ & $g(x)$ \\ \hline-2 & $\square$ \\ \hline-1 & $\square$ \\ \hline 0 & $\square$ \\ \hline 1 & $\square$ \\ \hline \end{tabular}