Questions: A chi-square distribution with 11 degrees of freedom is graphed below. The region under the curve to the right of (x0.755) is shaded. The area of this region is 0.755. Area = 0.755 Find the value of (x0.755). Round your answer to three decimal places. (x0.755 = )

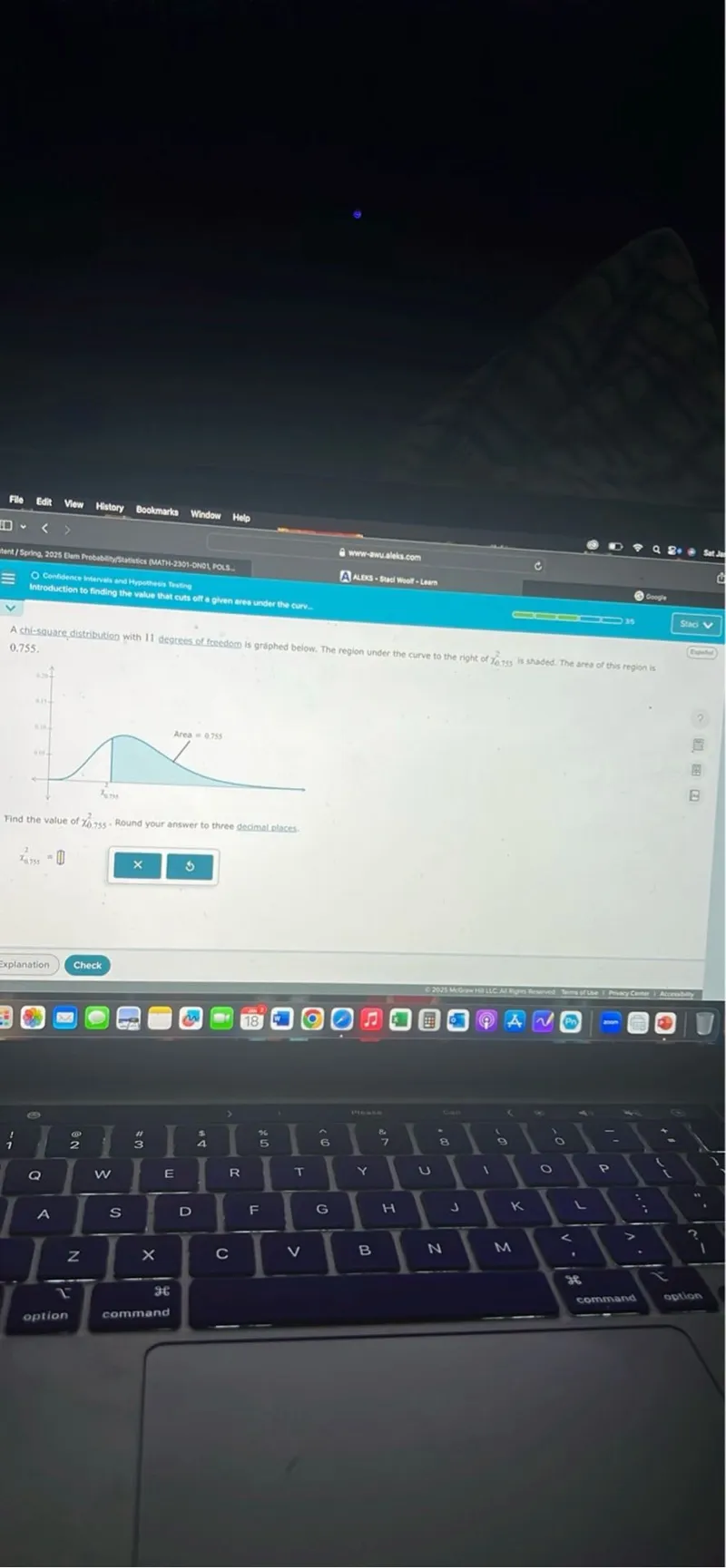
A chi-square distribution with 11 degrees of freedom is graphed below. The region under the curve to the right of (x0.755) is shaded. The area of this region is 0.755.

Area = 0.755

Find the value of (x0.755). Round your answer to three decimal places.

(x0.755 = )

Transcript text: A chi-square distribution with 11 degrees of freedom is graphed below. The region under the curve to the right of $x_{0.755}$ is shaded. The area of this region is 0.755. Area = 0.755 Find the value of $x_{0.755}$. Round your answer to three decimal places. $x_{0.755} = \square$

Solution

Solution Steps

Step 1: Identify the given information

We are given a chi-square distribution with 11 degrees of freedom. The area to the right of $ \chi^2_{0.755} $ is 0.755. We need to find the value of $ \chi^2_{0.755} $.

Step 2: Understand the problem

We are looking for the chi-square value ($ \chi^2_{0.755} $) such that the area to its right under the chi-square distribution curve with 11 degrees of freedom is 0.755. This means the cumulative probability up to $ \chi^2_{0.755} $ is $ 1 - 0.755 = 0.245 $.

Step 3: Use a chi-square table or calculator

Using a chi-square table or calculator (or statistical software) for 11 degrees of freedom and a cumulative probability of 0.245, we find the corresponding chi-square value.

Final Answer

$ \boxed{7.589} $

Was this solution helpful?

Unhelpful

Helpful

Questions asked by other users

< Previous Next >

Thank you for your feedback.

Copied!