Questions: Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value. lim (x -> 10) (x^2-100)/(x-10) Select the correct choice below and, if necessary, fill in the answer box within your choice. A. lim (x -> 10) (x^2-100)/(x-10)= (Simplify your answer.) B. The limit does not exist and is neither ∞ nor -∞.
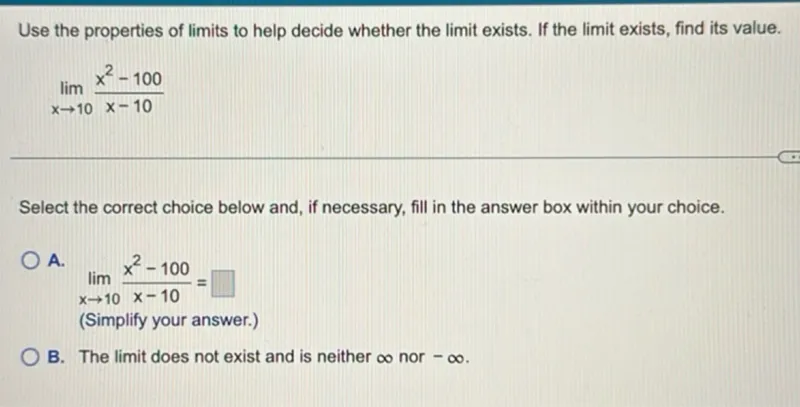
Transcript text: Use the properties of limits to help decide whether the limit exists. If the limit exists, find its value.
\[
\lim _{x \rightarrow 10} \frac{x^{2}-100}{x-10}
\]
Select the correct choice below and, if necessary, fill in the answer box within your choice.
A. $\lim _{x \rightarrow 10} \frac{x^{2}-100}{x-10}=$ $\square$
(Simplify your answer.)
B. The limit does not exist and is neither $\infty$ nor $-\infty$.
Solution
Was this solution helpful?
Answered
