Questions: Amanda has 14 coins in her pocket that equal 54 cents. All the coins are nickels, (n), and pennies, (p). Which combination of coins does Amanda have? Use the table to answer the question. Number of Coins nickels ((n)) pennies (p) (n+p=14) 5 9 14 8 6 14 10 4 14 11 3 14 - 5 nickels and 9 pennies - 8 nickels and 6 pennies - 10 nickels and 4 pennies - 11 nickels and 3 pennies

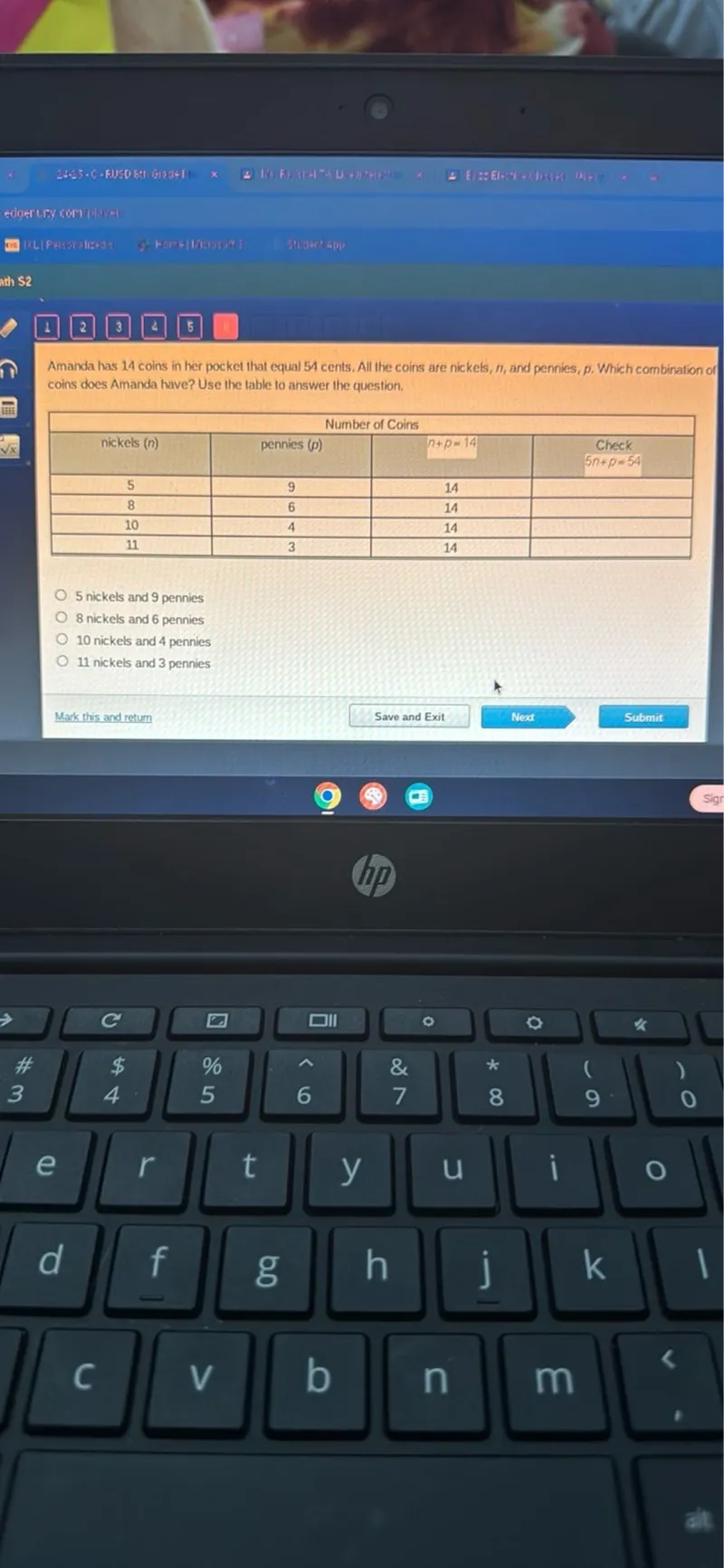
Amanda has 14 coins in her pocket that equal 54 cents. All the coins are nickels, (n), and pennies, (p). Which combination of coins does Amanda have? Use the table to answer the question.

Number of Coins
nickels ((n)) pennies (p) (n+p=14)
5 9 14
8 6 14
10 4 14
11 3 14

- 5 nickels and 9 pennies
- 8 nickels and 6 pennies
- 10 nickels and 4 pennies
- 11 nickels and 3 pennies

Transcript text: Amanda has 14 coins in her pocket that equal 54 cents. All the coins are nickels, $n$, and pennies, $p$. Which combination of coins does Amanda have? Use the table to answer the question. \begin{tabular}{|c|c|c|c|} \hline \multicolumn{4}{|c|}{ Number of Coins } \\ \hline nickels $(n)$ & pennies (p) & $n+p=14$ & \begin{tabular}{c} Check \\ \end{tabular} \\ \hline 5 & 9 & 14 & \\ \hline 8 & 6 & 14 & \\ \hline 10 & 4 & 14 & \\ \hline 11 & 3 & 14 & \\ \hline \hline \end{tabular} 5 nickels and 9 pennies 8 nickels and 6 pennies 10 nickels and 4 pennies 11 nickels and 3 pennies

Solution

Solution Steps

Step 1: Define the variables and equations

Let $ n $ represent the number of nickels and $ p $ represent the number of pennies. We are given two pieces of information:

The total number of coins is 14: \[ n + p = 14 \]
The total value of the coins is 54 cents: \[ 5n + p = 54 \]

Step 2: Solve the system of equations

We can solve the system of equations using substitution. From the first equation, we can express $ p $ in terms of $ n $: \[ p = 14 - n \] Substitute this into the second equation: \[ 5n + (14 - n) = 54 \] Simplify and solve for $ n $: \[ 5n + 14 - n = 54 \\ 4n + 14 = 54 \\ 4n = 40 \\ n = 10 \] Now, substitute $ n = 10 $ back into the equation $ p = 14 - n $: \[ p = 14 - 10 = 4 \]

Step 3: Verify the solution

Check that the total value of 10 nickels and 4 pennies is indeed 54 cents: \[ 5(10) + 4 = 50 + 4 = 54 \text{ cents} \] This matches the given total value.