Questions: Use the Product Rule to find the derivative of the given function. Find the derivative by multiplying the expressions first. y=x^6 * x^3 Use the Product Rule to find the derivative of the function. Select the correct answer below and fill in the answer box(es) to complete your choice. A. The derivative is () x^3+6 x^5. B. The derivative is (()(x^3)+(6 x^5) ). C. The derivative is ()(x^3) : D. The derivative is (x^6)()+x^3()). E. The derivative is ()(x^6).

Solution Steps

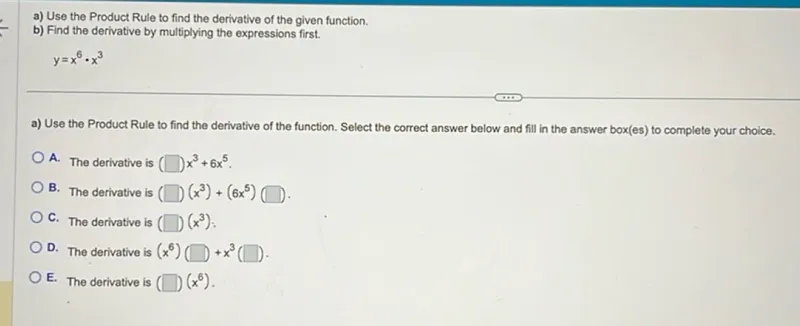
The Product Rule states that if \( y = u(x) \cdot v(x) \), then the derivative \( y' \) is given by: \[ y' = u'(x) \cdot v(x) + u(x) \cdot v'(x). \] For the given function \( y = x^{6} \cdot x^{3} \), let: \[ u(x) = x^{6}, \quad v(x) = x^{3}. \] The derivatives of \( u(x) \) and \( v(x) \) are: \[ u'(x) = 6x^{5}, \quad v'(x) = 3x^{2}. \] Applying the Product Rule: \[ y' = u'(x) \cdot v(x) + u(x) \cdot v'(x) = 6x^{5} \cdot x^{3} + x^{6} \cdot 3x^{2}. \] Simplify the expression: \[ y' = 6x^{8} + 3x^{8} = 9x^{8}. \]

Alternatively, we can simplify the original function before taking the derivative: \[ y = x^{6} \cdot x^{3} = x^{6+3} = x^{9}. \] Now, take the derivative of \( y = x^{9} \): \[ y' = 9x^{8}. \]

The derivative calculated using both methods is \( y' = 9x^{8} \). Comparing this with the given options:

• Option A: The derivative is \( (\square) x^{3} + 6x^{5} \).
• Option B: The derivative is \( (\square)(x^{3}) + (6x^{5})(\square) \).
• Option C: The derivative is \( (\square)(x^{3}) \).
• Option D: The derivative is \( (x^{6})(\square + x^{3}(\square)) \).
• Option E: The derivative is \( (\square)(x^{6}) \).

None of the options directly match \( y' = 9x^{8} \). However, the correct derivative is \( y' = 9x^{8} \).

Final Answer