Questions: Harry took out a loan from the bank. The variable D models Harry's remaining debt (in dollars) t months after he took out the loan. D = -200 t + 9000 How much does Harry pay back each month?

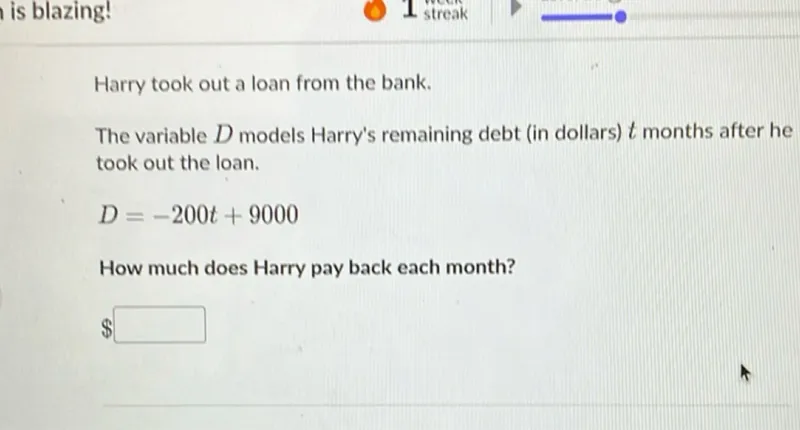
Harry took out a loan from the bank. The variable D models Harry's remaining debt (in dollars) t months after he took out the loan.
D = -200 t + 9000

How much does Harry pay back each month?

Transcript text: Harry took out a loan from the bank. The variable $D$ models Harry's remaining debt (in dollars) $t$ months after he took out the loan. \[ D=-200 t+9000 \] How much does Harry pay back each month?

Solution

Solution Steps

Step 1: Understand the Equation

The equation given is $ D = -200t + 9000 $, where $ D $ represents Harry's remaining debt in dollars, and $ t $ represents the number of months after he took out the loan. The equation is in the form of a linear equation $ y = mx + b $, where $ m $ is the slope.

Step 2: Identify the Slope

In the equation $ D = -200t + 9000 $, the slope $ m $ is $-200$. The slope represents the rate of change of the debt with respect to time. In this context, it indicates how much the debt decreases each month.

Step 3: Interpret the Slope

The slope $-200$ means that Harry's debt decreases by $200 each month. Therefore, Harry pays back $200 each month.